W zeszłym miesiącu Polskie Sieci Elektroenergetyczne zakomunikowały, że odnotowały rekordowe zapotrzebowanie na moc elektryczną w szczycie porannym okresu letniego. No cóż, czerwiec był wyjątkowo gorącym miesiącem, stąd nie ma się co dziwić, że zapotrzebowanie na energię elektryczną było również ogromne.
Czy tak wysokie zapotrzebowanie na energię elektryczną można było przewidzieć wcześniej? Oczywiście, prognozę zużycia energii elektrycznej uważa się za przykład takich prognoz, gdzie dobrze rozumiemy czynniki wpływające na zapotrzebowanie na energię, mamy dość sporą ilość danych historycznych i co więcej potrafimy skonstruować dobry jakościowo model wiążący zapotrzebowanie na energię elektryczną z kluczowymi zmiennymi. Dziś spróbujemy zatem przewidzieć zapotrzebowanie na energię elektryczną na podstawie danych historycznych zgodnie z powiedzeniem, że jeden wykres powie nam więcej niż tysiąc słów.
Do prognozy przyszłego zużycia energii elektrycznej skorzystamy z danych pochodzących od operatora sieci elektroenergetycznych PSE. Firma na swoich stronach publikuje dość szeroki wachlarz informacji na temat funkcjonowania Krajowego Systemu Elektroenergetycznego i Rynku Bilansującego. Na potrzeby analizy wykorzystam dane o strukturze produkcji energii elektrycznej w elektrowniach krajowych, wielkości wymiany energii elektrycznej z zagranicą i w konsekwencji dane o krajowym zużyciu energii elektrycznej w układzie miesięcznym począwszy od stycznia 2005 roku.
Nasze prognozowanie będzie tzw. predykcją szeregu czasowego. Co to jest szereg czasowy? To nic innego jak obserwacje interesującej nas wielkości zarejestrowane w kolejnych (zazwyczaj regularnych) odstępach czasu, np. mogą to być dni, tygodnie, miesiące, kwartały, lata itp. Kolejne obserwacje szeregu czasowego charakteryzują się nieprzypadkowym porządkiem i wykazują zazwyczaj istotną korelację. I ta korelacja pomiędzy obserwacjami jest wykorzystywana do prognozowania przyszłych wartości szeregu czasowego. Polecam pozycję literaturową Forecasting: Principles and Practice autorstwa Roba J Hyndmana i George Athanasopoulosa.
To będzie długi wpis, w tym trochę matematyki również się znajdzie, zatem warto wpierw zaparzyć sobie kawę lub herbatkę. Jak jesteście gotowi to bierzmy się do pracy.
Wpierw pobieramy dane i wczytujemy je do środowiska R. Ponieważ szereg czasowy wymaga odpowiedniej reprezentacji w środowisku komputerowym dokonujemy następnie przekształcenia do klasy ts (time series), która to właśnie jest podstawową strukturą wykorzystywaną w R do reprezentacji szeregów czasowych. Do prognozowania korzystać będziemy z funkcji umieszczonych w bibliotece forecast.
library(tidyverse)
library(readxl)
library(forecast)
library(tsbox)
# pobieramy dane z Excela
plik <- "produkcja_zuzycie_energii_elektrycznej.xlsx"
# pobieramy dane z odpowiedniego zakresu komórek
produkcja <- t(read_excel(plik, sheet = 1, range = "B3:FR3", col_names = FALSE))
saldo <- t(read_excel(plik, sheet = 1, range = "B13:FR13", col_names = FALSE))
zuzycie <- t(read_excel(plik, sheet = 1, range = "B14:FR14", col_names = FALSE))
# tworzymy szeregi czasowe
produkcja.ts <- ts(produkcja, start = c(2005,1), frequency = 12)
saldo.ts <- ts(saldo, start = c(2005,1), frequency = 12)
zuzycie.ts <- ts(zuzycie, start = c(2005,1), frequency = 12)
Mając przygotowane dane możemy je sobie wyświetlić.
# dane jako ramka dla ggplot do wykreslenia wielkosci produkcji, salda i zuzycia
produkcja.ts.df <- ts_df(produkcja.ts)
saldo.ts.df <- ts_df(saldo.ts)
zuzycie.ts.df <- ts_df(zuzycie.ts)
# wykres produkcji energii elektrycznej ogółem oraz salda wymiany międzynarodowej
ggplot() +
geom_line(data=produkcja.ts.df,aes(x = time, y = value)) +
geom_line(data=saldo.ts.df,aes(x = time, y = value)) +
geom_hline(yintercept = 0, color="red") +
theme_tsbox() +
ggtitle("Produkcja energii elektrycznej ogółem oraz saldo wymiany międzynarodowej [GWh]") +
xlab("Lata") + ylab("Ilość energii [GWh]")
Analiza danych dotyczących produkcji elektrycznej może nam dość sporo powiedzieć o tym, jak kształtowało się zapotrzebowanie na energię, jaki jest długoterminowy trend i czy występują okresowe wahania. To z pewnością ważne informacje dla sektora energetycznego. Zobaczmy zatem jak to wyglądało na przestrzeni ostatnich kilkunastu lat.
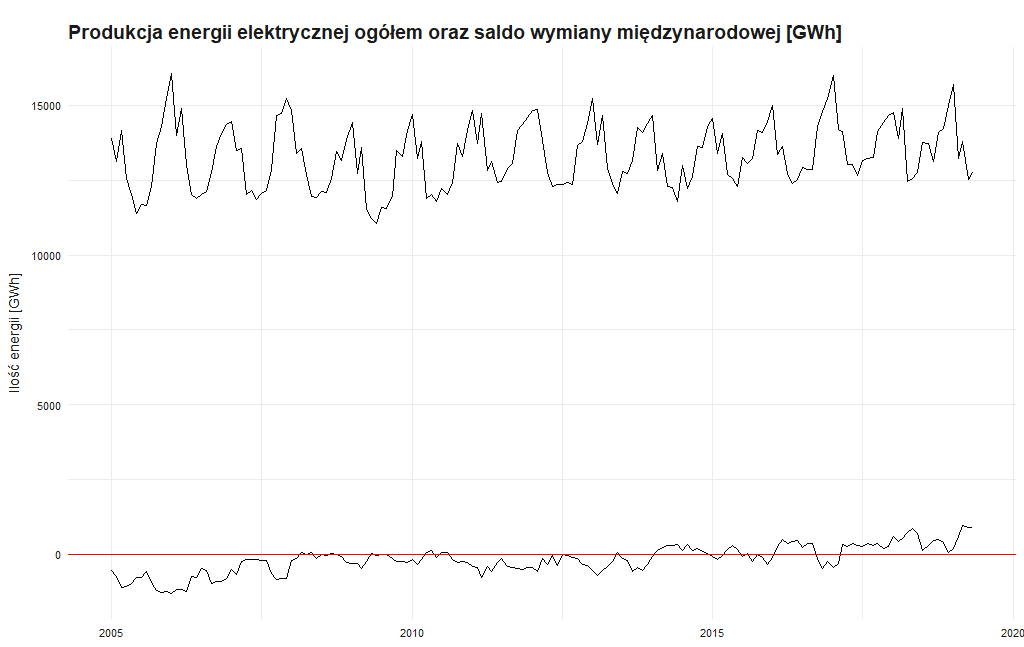
Wykres przedstawia produkcję energii elektrycznej w polskich jednostkach wytwórczych oraz saldo wymiany międzynarodowej. Przyglądając się wykresowi produkcji energii elektrycznej łatwo zauważyć, że dane ulegają sezonowym zmianom. W okresie zimowym zapotrzebowanie na energię elektryczną jest znacznie wyższe niż latem. Oczywiście wiąże się to z krótszym dniem w okresie zimowym, a przez to koniecznością używania oświetlenia jak również ogrzewaniem lub dogrzewaniem pomieszczeń. Z kolei analizując wykres salda niepokojące jest to, że o ile do roku 2015 byliśmy eksporterem energii elektrycznej, to praktycznie od 2017 jesteśmy jego importerem i to nawet w okresie letnim. Świadczy to, że nasze moce wytwórcze są coraz w mniejszym stopniu gotowe by pokryć zapotrzebowanie na energię elektryczną, a jak pokazano poniżej jest ono w wyraźnym trendzie wzrostowym.
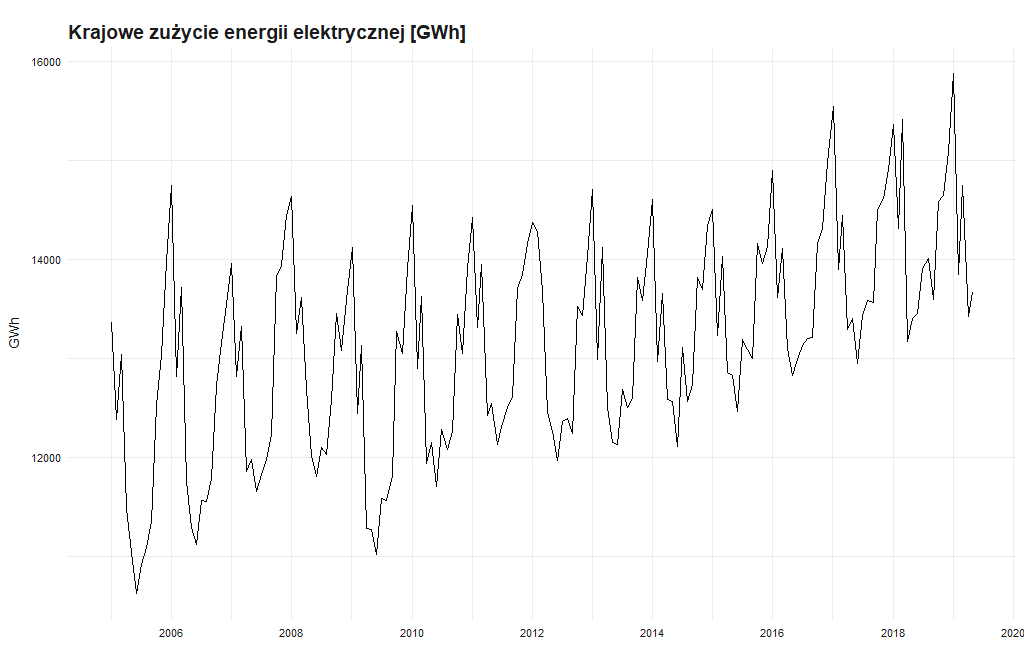
By sprawdzić jak na przestrzeni lat 2005-2019 zmieniało się zużycie energii elektrycznej w poszczególnych miesiącach zerknijmy na poniższy wykres wygenerowany przez następujący kod:
ggsubseriesplot(zuzycie.ts) +
xlab("Miesiące") + ylab("GWh") +
ggtitle("Zużycie energii elektrycznej w poszczególnych miesiącach na przestrzeni lat 2005-2019")
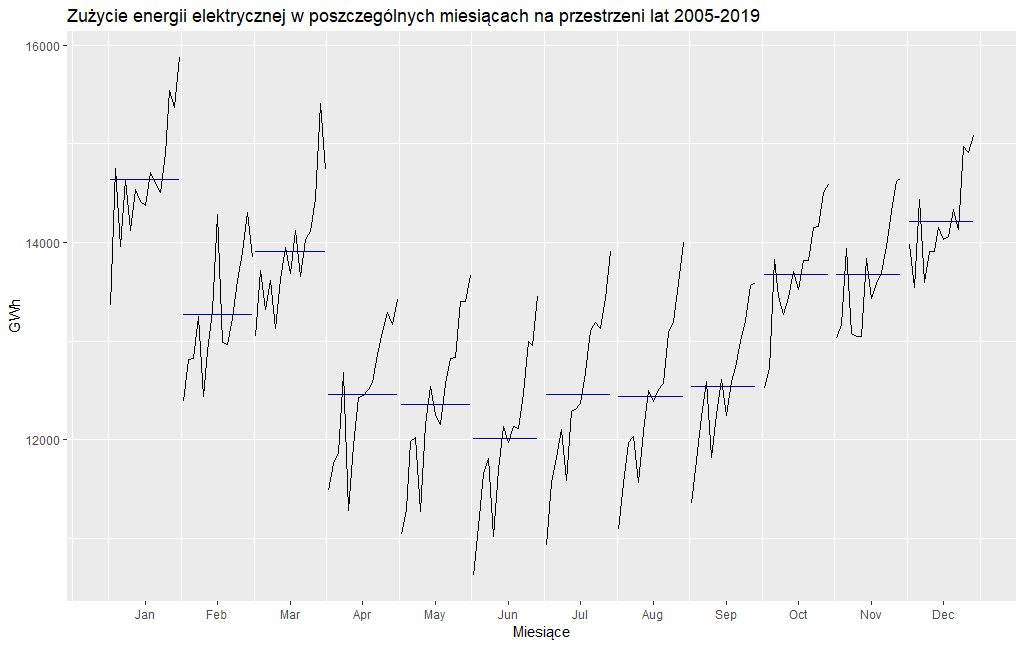
Niebieskie poziome linie przedstawiają średnie wartości produkcji prądu w danym miesiącu z lat analizy. Jak widać, w przypadku praktycznie wszystkich miesięcy mieliśmy do czynienia z bardzo podobnymi zmianami. Odnotowaliśmy spadek w 2009 roku, a następnie systematyczny wzrost. Przy czym o ile jeszcze dla miesięcy zimowych dla poszczególnych lat można odnaleźć niewielkie wahnięcia, to w przypadku miesięcy letnich z roku na rok zużycie energii elektrycznej jest coraz większe. Dość dobrze można to dostrzec na kolejnym wykresie. Dla przejrzystości analizę ograniczyłem do ostatnich dziesięciu lat.
zuzycie.ts.5y = window(zuzycie.ts, start = c(2010,1))
ggseasonplot(zuzycie.ts.5y, year.labels = TRUE, year.labels.left = FALSE, col = rainbow(10), labelgap = 0.03) +
ggtitle("Sezonowe zużycie energii elektrycznej - ostatnie 10 lat") +
xlab("Miesiące") + ylab("GWh") +
theme(legend.position = "bottom") +
theme_minimal()
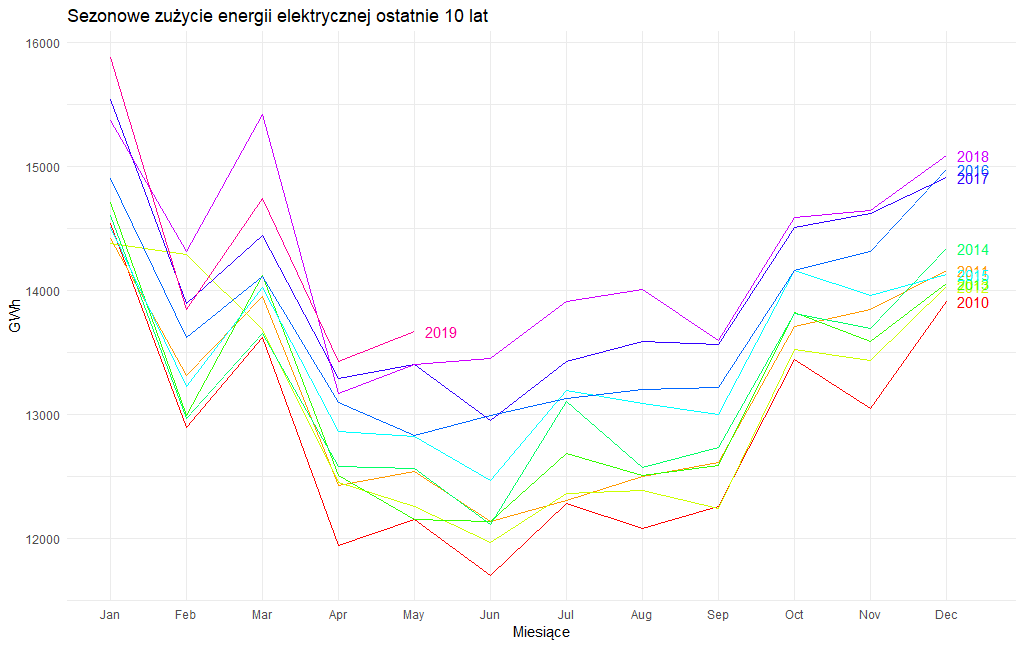
Obserwujemy widoczną sezonowość w zużyciu energii. Zdecydowanie większe zużycie energii występuje w zimowych miesiącach, w lecie mamy spadek, ale jak przyjrzymy się legendzie z prawej strony przy liniach to z każdym kolejnym rokiem to zużycie energii w miesiącach letnich jest coraz większe. Jak widać zmiany klimatycznie nie pozostają bez wpływu na zapotrzebowanie na energię elektryczną, w tym przypadku w szczególności dla chłodzenia.
Jedyne co może przeszkadzać na tym wykresie, to uskok w miesiącu lutym, teoretycznie miesiącu, który jest zimniejszy od marca. Ale jeżeli zwrócimy uwagę, że podane przez KSE zużycie energii jest określone jako sumaryczne w danym miesiącu i luty, jakby nie było ma w większości przypadków aż o trzy dni mniej niż styczeń i marzec to nie pozostaje nic innego jak koniecznie przeprowadzić dopasowanie kalendarzowe po to by dopasować nasze dane do zmieniającej się ilości dni w poszczególnych miesiącach. Zastosowanie takiej korekty efektów kalendarzowych (month-length adjustment) może uchronić przed błędnym zinterpretowaniem jako wahań sezonowych pokazanych na wykresie spadków w lutym, które są związane wyłącznie z długością danego miesiąca. W tym celu skorzystam z funkcji monthdays().
# zauważalny spadek w lutym kazdego roku, mniejsza liczba dni, nalezy skorygowac
av.days <- 365.25/12
m.days <- monthdays(zuzycie.ts)
zuzycie.ts.adj <- zuzycie.ts/m.days*av.days
i w rezultacie po takiej korekcie nasz wykres wygląda następująco.
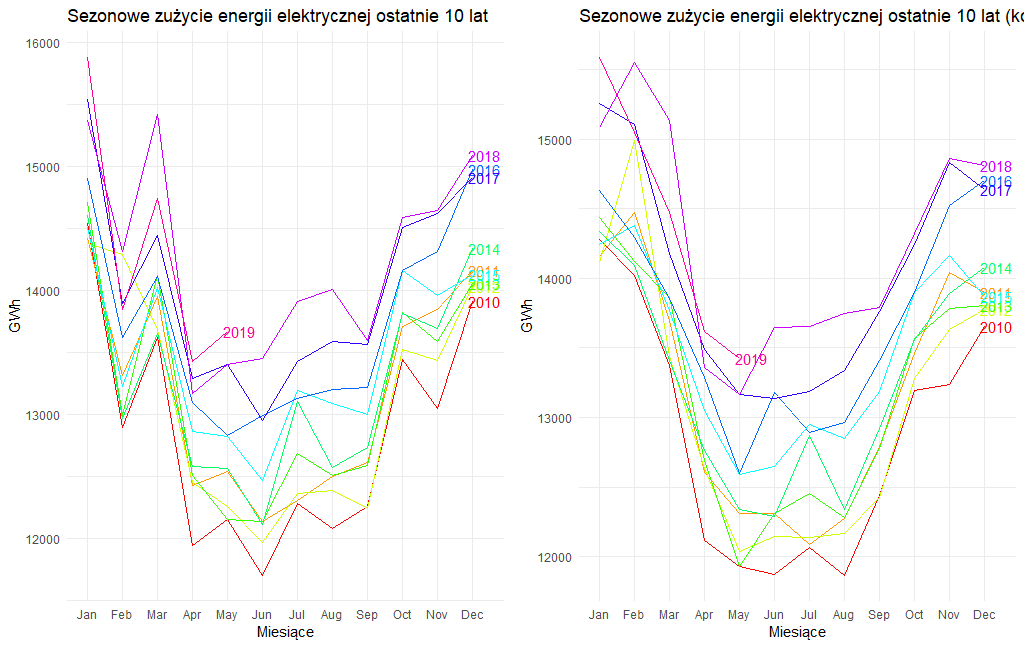
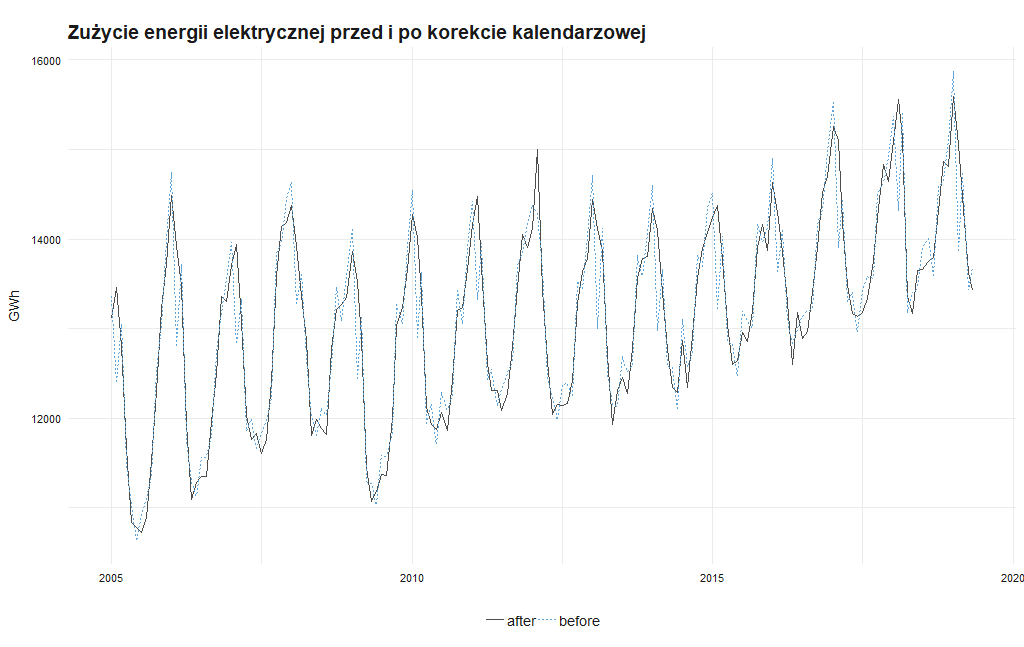
W wyniku dopasowania wykres stał się gładszy. Do dalszej analizy wykorzystane zostaną dane uwzględniające korektę kalendarzową. Zresztą by zobaczyć różnicę w wykresie zużycia energii elektrycznej wato nałożyć jeden wykres na drugi.
zuzycie.df <- ts_df(ts_c(before=zuzycie.ts,after=zuzycie.ts.adj))
ggplot(zuzycie.df, aes(x = time, y = value)) +
geom_line(aes(linetype = id,col=id)) +
theme_tsbox() +
scale_color_tsbox()
Istotnym pytaniem w analizie szeregu czasowego jest to, czy występuje i jak silna jest korelacja czasowa w danych, czyli tzw. autokorelacja. Aby to zbadać wykreślę wykres autokorelacji ACF.
ggAcf(zuzycie.ts.adj, lag = 48)
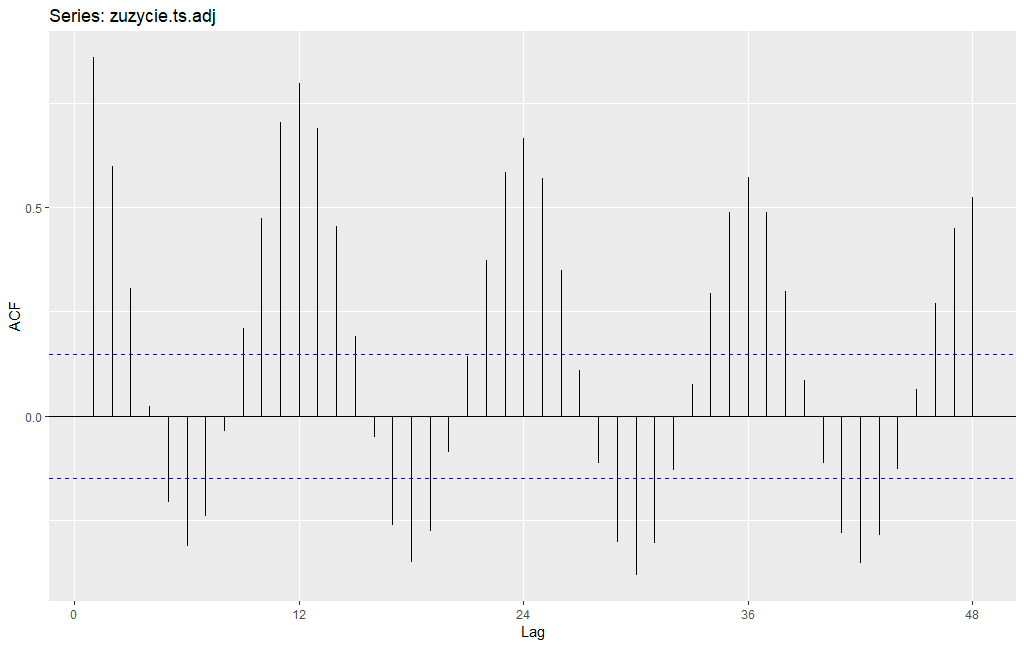
To co widzimy na wykresie autokorelacji to po pierwsze bardzo wolno zanikającą funkcję z wyraźną okresowością występowania. Tym okresem dla tego przypadku jest liczba 12, czyli mamy do czynienia z sezonowością roczną. Uzyskany wynik potwierdza obecność w szeregu występowanie trendu długoterminowego oraz sezonowości. Te ustalenia mają bardzo ważne przełożenie na zdefiniowanie szeregu jako stacjonarny lub niestacjonarny, a to determinuje sposób postępowania przy modelowaniu oraz konstruowaniu prognoz. Zresztą aby lepiej zrozumieć naturę analizowanego szeregu czasowego pomocne jest by wyodrębnić z niego regularne składowe, czyli długoterminowy trend oraz sezonowość. Ważne znaczenie ma także analiza własności losowych fluktuacji (szumu). Takie postępowanie określa się jako dekompozycja szeregu i w programie R możemy je przeprowadzić poprzez wykorzystanie funkcji decompose() z biblioteki stats. O dekompozycji szeregu czasowych można także poczytać w książce Analiza i prognozowanie szeregów czasowych Adama Zagdańskiego i Artura Suchwałko wydanej nakładem wydawnictwa PWN.
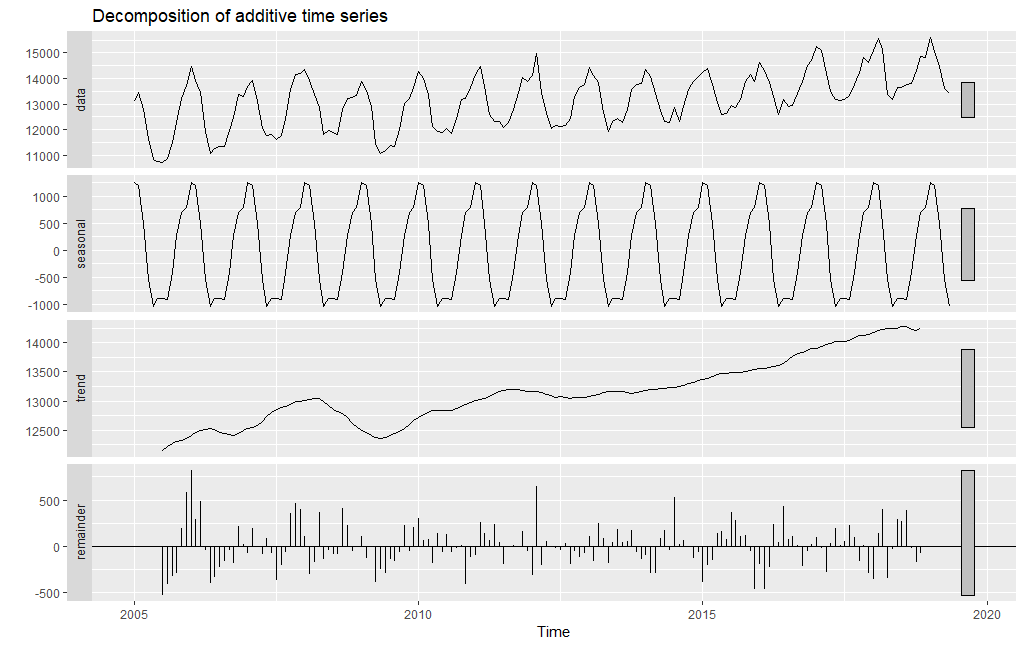
Symbolicznie model dekompozycji możemy przedstawić za pomocą równań:
Yt = Tt + St + Et (dekompozycja addytywna) lub
Yt = Tt x St x Et (dekompozycja multiplikatywna)
gdzie: Tt – trend; St – sezonowość; Et – losowe fluktuacje
Dla danych zużycia energii zastosowana została dekompozycja addytywna, gdyż amplituda wahań sezonowych lub wariancja wokół tendencji długoterminowej nie zmienia się wraz z poziomem szeregu. Analiza wykresu pozwala jasno potwierdzić, że w analizowanym szeregu czasowym występuje długoterminowy trend i wyraźny wzorzec sezonowości rocznej. Trend odpowiada długofalowej tendencji, wzrostu ze względu na coraz większą liczbę urządzeń elektrycznych, sezonowość – to zużycie związane z porą roku, a fluktuacje to wszystkie inne zdarzenia. W naszym przypadku z uwagi na to, że mamy trend i sezonowość to mamy do czynienia z szeregiem niestacjonarnym. To istotna informacja, gdyż w analizie szeregów czasowych krytyczne znaczenie ma wybór odpowiedniego modelu matematycznego do danych. I tak dla szeregów stacjonarnych możemy stosować klasyczne modele stacjonarne takie jak: biały szum o średniej zero i wariancji s2, model autoregresji – AR(p), model ruchomej średniej MA(q), model mieszany autoregresji rzędu p, ruchomej średniej rzędu q -ARMA(p,q), sezonowy model autoregresji rzędu P, ruchomej średniej rzędu Q – ARMA(P,Q) czy połączony model ARMA(p,q) i model sezonowy ARMA(P,Q) czyli ARMA(p,q)x(P,Q)s, dla szeregów niestacjonarnych ARIMA(p,d,q), sezonową odmianę SARIMA(p,d,q)x(P,D,Q)s. Alternatywnym podejściem jest model dekompozycji, a także ważną rodzinę modeli (ponad trzydzieści różnych wariantów) stanowią modele oparte na wygładzaniu wykładniczym ETS. O tych modelach i doboru parametrach do nich można przeczytać we wspomnianej już książce.
Z uwagi na to, że nasz szereg jest niestacjonarny tak jak i praktycznie 95% innych szeregów czasowych skorzystamy z modeli przewidzianych dla tego rodzaju szeregu. Oczywiście nic nie stoi na przeszkodzie by najpierw próbować przekształcić nasz szereg do postaci szeregu stacjonarnego np. za pomocą transformacji Boxa-Coxa i różnicowania, ale może o tym kiedy indziej. Dziś skoncentrujemy się na modelu ARIMA, modelu dekompozycji oraz modelu wygładzania wykładniczego ETS. By sprawdzić, który z wymienionych modeli jest najbardziej adekwatny do prognozowania przyszłych wartości musimy go przetestować. Technika jest taka, by posiadany zbiór danych podzielić na dwie grupy, tzw. zbiór uczący oraz zbiór testowy. Zbiór uczący zostanie wykorzystany do zbudowania określonych modeli, które wykorzystamy do dokonania prognozy na następne okresu. Te prognozy porównamy ze zbiorem testowym, czyli z rzeczywistymi danymi. Zbiór uczący będzie zatem zawierał zużycie energii elektrycznej z okresu styczeń 2005 – grudzień 2015, a zbiór testowy stanowić będzie dane z okresu styczeń 2016 – czerwiec 2019. To do dzieła, dzielimy dane na dwie grupy.
zuzycie_train_ts <- window(zuzycie.ts.adj, end=c(2015,12))
zuzycie_test_ts <- window(zuzycie.ts.adj, start=c(2016,1))
horyzont <- length(zuzycie_test_ts)
Graficznie wygląda to tak:
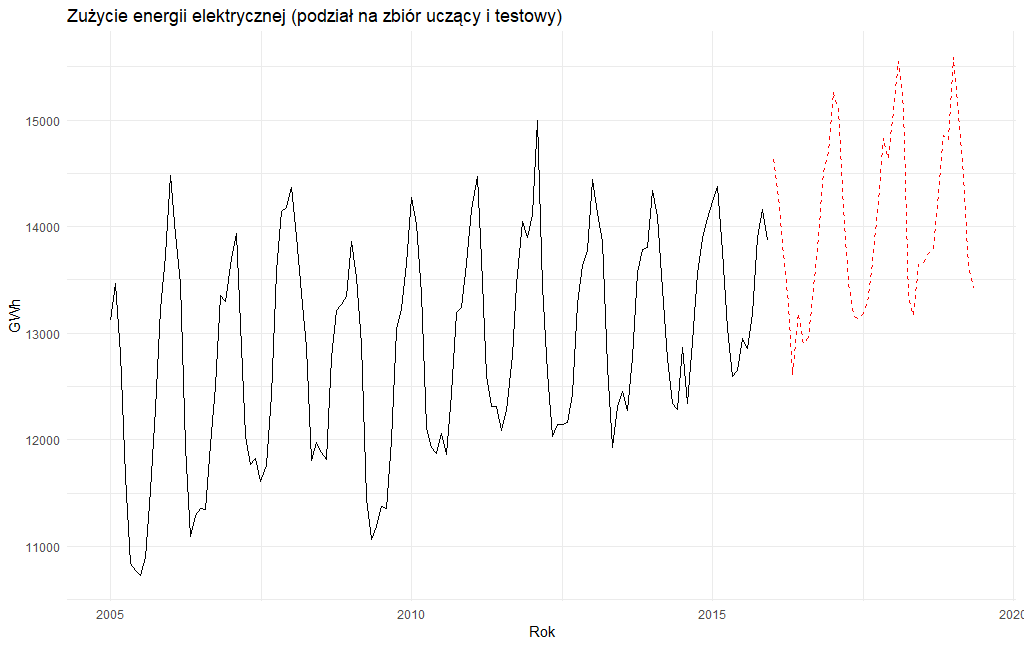
Optymalny wariant wybierzemy na podstawie oceny kryterium informacyjnego (AIC, AICC, BIC), czyli tzw. kryterium oceniającego dobroć dopasowania oraz na podstawie kryterium błędów „RMSE”, „MAE”, „MAPE” oraz „MASE”, czyli kryterium oceniającego dokładność prognoz.
- AIC (Akaike Information Criterion) – ma tendencje do przeszacowania rzędu modeli
- AICC (Corrected AIC) – skorygowany AIC by wyeliminować wspomnianą tendencję
- BIC (Bayesian Information Criterion) – model może prowadzić do asymptotycznie optymalnych prognoz
Bez względu na to, które kryterium wybierzemy kierujemy się jego minimalizacją, czyli wybieramy ten model, dla którego wartość kryterium jest mniejsza.
- RMSE (Root Mean Squared Error)
- MAE (Mean Absolute Error)
- MAPE (Mean Absolute Percentage Error)
- MASE (Mean Absolute Scaled Error)
Trzeba zaznaczyć, że kryterium oparte na błędach nie ma wbudowanego mechanizmu, który karałby za zbyt skomplikowany model. Zatem im bardziej skomplikowany, bardziej dopasowany, model to błędy będą mniejsze. Zatem kierowanie się tymi wartościami może grozić ryzykiem nadmiernego dopasowania (tzw. overfitting), co może negatywnie odbić się potem na jakości naszej prognozy.
Dopasowanie modelu prognozy
- Prognoza na bazie dekompozycji
Konstrukcja prognozy polega na oszacowaniu składowej trendu oraz sezonowości, eliminacji trendów i wyznaczeniu szeregu reszt, dla którego dopasowujemy model stacjonarny z rodziny ARMA. W środowisku R do konstrukcji prognoz na podstawie dekompozycji możemy wykorzystać funkcję tslm() z biblioteki forecast. Dzięki tej funkcji łatwo zbudować model regresji uwzględniający jedynie trend, jedynie sezonowość lub oba te składniki razem. Ponieważ w naszym szeregu występuje zarówno trend, jak i sezonowość uwzględnimy oba te składniki.
model.tslm <- tslm(zuzycie_train_ts ~ trend + season)
summary(model.tslm)
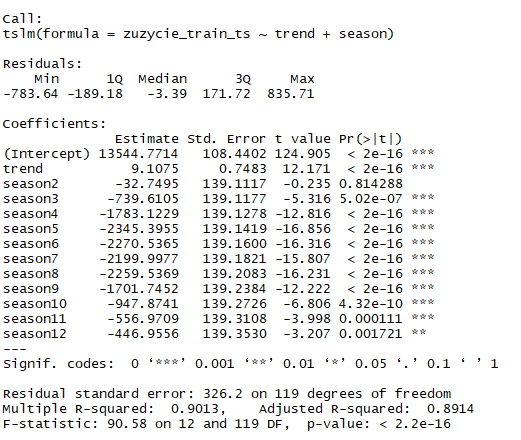
Wartość współczynnika dopasowania (R2) jest wysoka i wynosi 0,89. Także model wydaje się być dobrze dopasowany. Aby sprawdzić poprawność dopasowania wykorzystamy podstawowe narzędzia diagnostyczne jakim jest wykres ACF dla reszt oraz test losowości Ljung-Boxa. Wykres funkcji autokorelacji dla reszt z modelu dekompozycji przedstawia poniższy wykres.
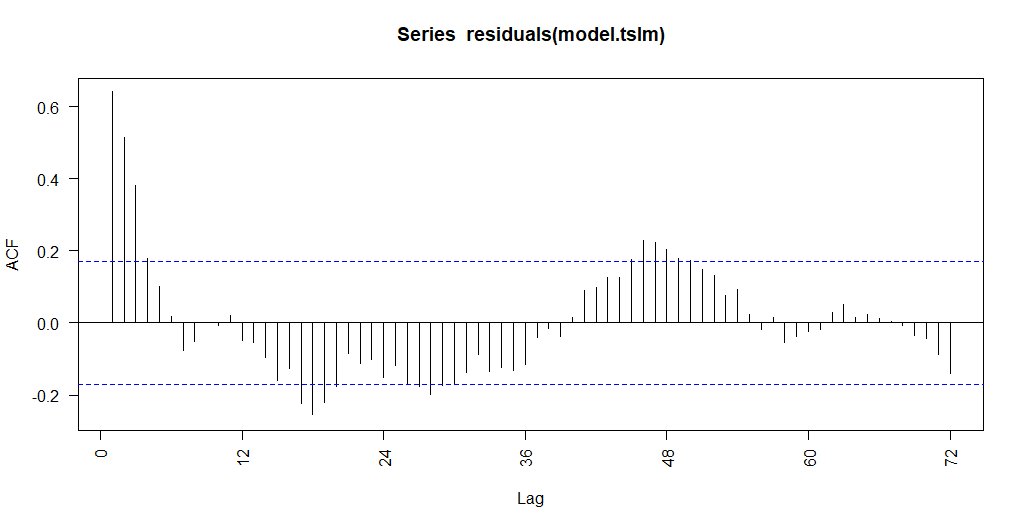

Jak widać wyniki testów wskazują na pozostałości korelacji w resztach z modelu dekompozycji. Stąd należałoby poprawić model, np. poprzez zastosowanie innego rodzaju trendu, np. wyższego stopnia. Zróbmy to zatem i zastosujmy trend wielomianowy drugiego i trzeciego stopnia.
model.tslm3 <- tslm(zuzycie_train_ts ~ season + trend + poly(trend,3,raw = TRUE))
Oczywiście im wyższy trend tym dopasowanie stawało się lepsze, wartość skorygowanego współczynnika dopasowania rosła, dla trendu wielomianowego stopnia trzeciego wynosiła R2 = 0,9094. Reszty modelu dla tego rodzaju trendu też były najbliższe spełnieniu założenia o stacjonarności. Także wykorzystując ten model uwzględniający trend wielomianowy trzeciego stopnia przeprowadzimy obecnie prognozy dla okresu testowego, czyli okresu styczeń 2016 – czerwiec 2019.
zuzycie.forecast.tslm <- forecast(model.tslm3, h = horyzont)
Wynik jest następujący:
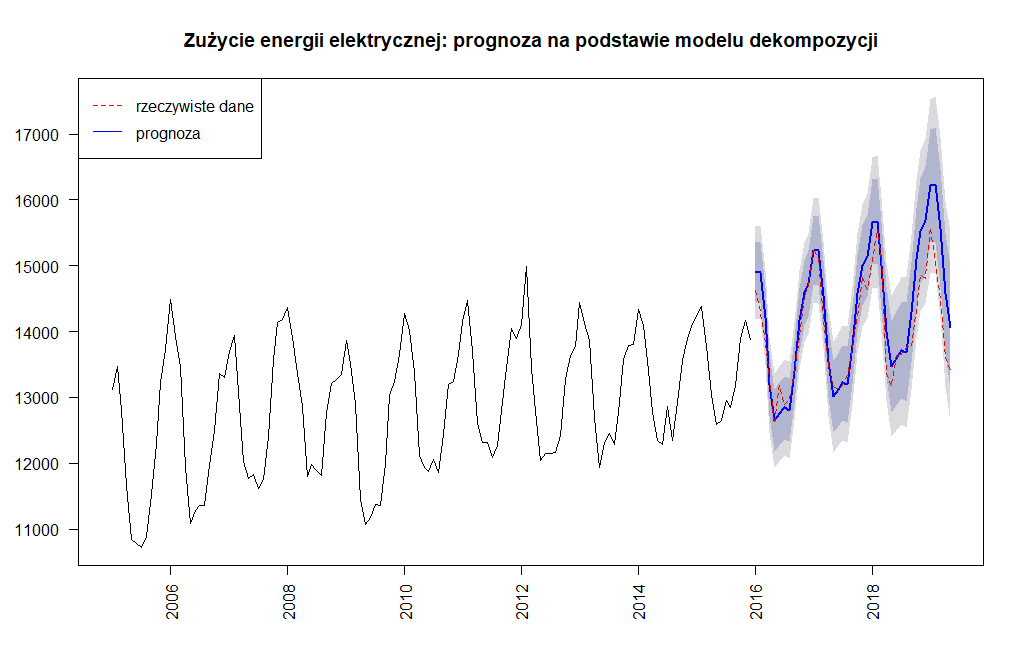
Dla wyjaśnienia określonego rodzaju tła, wyrażonego takim ciemniejszym i jaśniejszym kolorem, który pojawił się za niebieską linią prognozy. Linia niebieska to nic innego, jak konkretna wartość wyznaczana w oparciu o model. Nie mniej jednak trudno przewidzieć prognozowaną wartość dokładnie w punkt. Stąd często nie interesuje nas konkretna wartość, a pewien zakres wartości, w którym z odpowiednio wysokim prawdopodobieństwem znajduje się prognozowana wartość. Te przedziały określa się przedziałem predykcyjnym, przy czym długość tego przedziału uzależniona jest od prawdopodobieństwa (poziomu ufności). Najczęściej w praktyce stosowane wielkości prawdopodobieństwa to 80 i 95%. Zatem to ciemne tło uwzględnia prognozowane wartości z 80% prawdopodobieństwem, a to jaśniejsze z prawdopodobieństwem 95%.
Jak widać początkowo krzywa obrazująca prognozę dość dobrze współgrała z rzeczywistymi wartościami, w ostatnim roku prognoza znacząco nam się rozjechała. Dokładność prognozy oceniono wykorzystując podstawowe kryteria zaimplementowane w funkcji accuracy().
kryteria <- c("RMSE","MAE","MAPE","MASE")
accuracy(zuzycie.forecast.tslm,zuzycie_test_ts)[,kryteria]

2. Prognoza z wykorzystaniem wygładzania wykładniczego
Wygładzanie wykładnicze ETS (ang. ExponenTial Smoothing) to metody, które polegają na wygładzaniu nieregularnych fluktuacji w danych. Idea jest taka, że przypisuje się wykładniczo zanikające wagi obserwacjom z poprzednich okresów. W grupie tych modeli wyróżnia się ponad trzydzieści różnych wariantów. Model ETS składa się z równania różnicowego opisującego zmianę (ewolucję) oraz założenia o rozkładzie czynnika losowego. W środowisku R modele ETS realizowane są przez funkcję ets() z pakietu forecast. Optymalny wariant modelu wybierany jest poprzez minimalizację kryterium informacyjnego AICC a parametry wygładzające dobrane zostaną na podstawie minimalizacji błędu predykcji jednokrokowej, czyli np. kryterium MSE.
model.ets <- ets(zuzycie_train_ts, model="MAA",opt.crit = "mse", ic="aicc")
summary(model.ets)
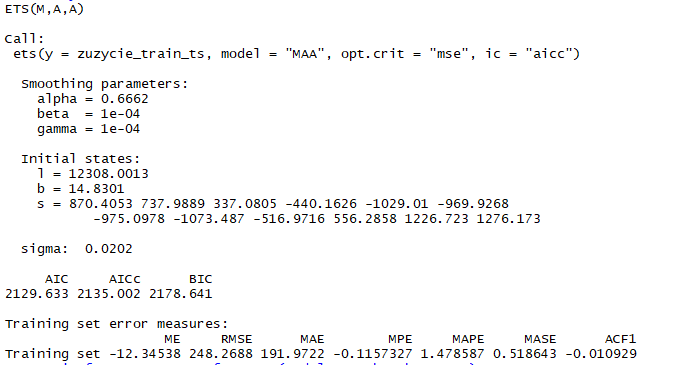
W oparciu zatem o obliczony model dokonamy prognozy dla okresu testowego.
zuzycie.forecast.ets <- forecast(model.ets, h = horyzont)
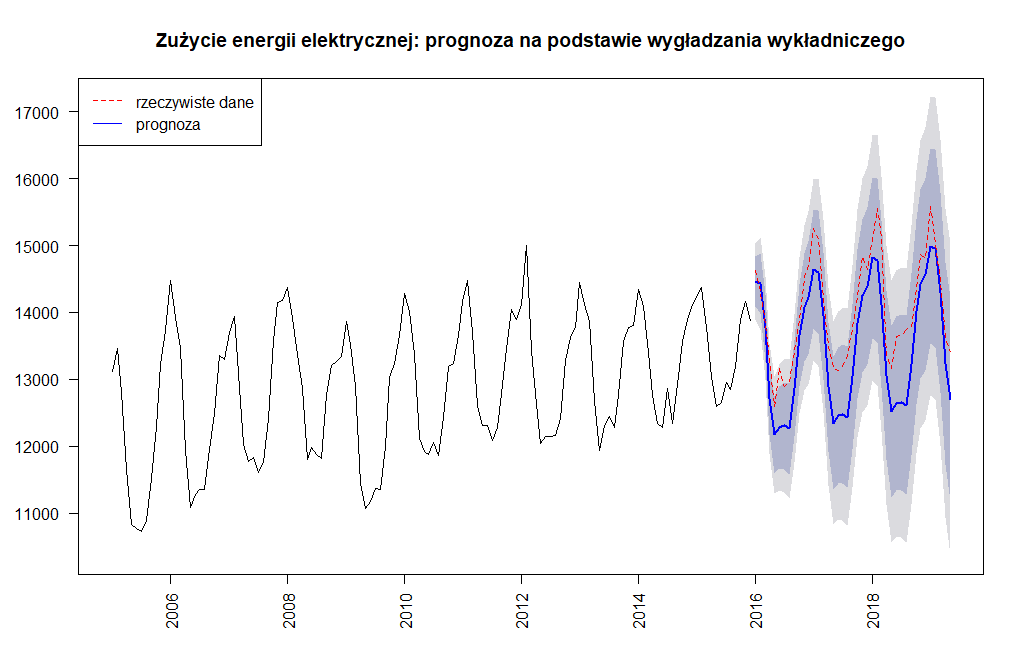
Na pierwszy rzut oka wygląda to znacznie gorzej niż w przypadku modelu dekompozycji. Praktycznie wartości rzeczywiste z prognozą dość mocno się rozjechały zachowując jedynie kształt. No cóż można stwierdzić, że ekstrapolacja trendu na kolejne okresy z wykorzystaniem modelu wygładzania wykładniczego nie dała zadowalających wyników. Obliczmy jeszcze kryteria dokładności prognozy.
accuracy(zuzycie.forecast.ets,zuzycie_test_ts)[,kryteria]

3. Prognoza na bazie modelu ARIMA
Prognozowanie na podstawie modeli należących do rodziny ARIMA obejmuje zarówno modele stacjonarne: MA(q), AR(p) czy ARMA(p,q) jak i modele niestacjonarne: zwykła ARIMA(p,d,q) oraz sezonowa SARIMA(p,d,q)x(P,D,Q)s. W środowisku R do opracowania prognoz można wykorzystać funkcję Arima() z pakietu forecast. Jak już wiemy nasz szereg jest szeregiem czasowym zawierającym składową trendu oraz sezonowość. Więc aby skorzystać z metod stacjonarnych musimy nasz szereg najpierw przekształcić do postaci stacjonarnej. Dokonamy wpierw transformacji Boxa-Coxa by spróbować wyeliminować niestacjonarność szeregu. Taka transformacja jest potrzebna wówczas gdy:
- występuje wzrost lub spadek amplitudy wahań sezonowych
- mamy niejednorodną zmienność w kolejnych okresach
- mamy obserwacje odstające.
Jak wynika z analizy wykresu zużycia energii takie sytuacje w naszym szeregu nie występują, ale mimo to przeprowadźmy tą operację dla dwóch wartości parametru l (l = 0 – transformacja logarytmiczna, l = 0.5 – transformacja pierwiastkowa). Do przeprowadzania operacji wykorzystamy funkcję BoxCox() z pakietu forecast, a następnie wykreślimy obok siebie szeregi by zaobserwować czy zaszły w nich jakieś zmiany.
par(mfrow=c(3,1))
plot(zuzycie.ts.adj,main="Oryginalne dane",xlab="",ylab="")
grid()
plot(BoxCox(zuzycie.ts.adj, lambda = 0.5),
main="Dane po transformacji Boxa-Coxa (lambda =0,5 - transformacja pierwiastkowa)",
xlab="",ylab="")
grid()
plot(BoxCox(zuzycie.ts.adj, lambda = 0),
main="Dane po transformacji Boxa-Coxa (lambda = 0 - transformacja logarytmiczna)",
xlab="",ylab="")
grid()
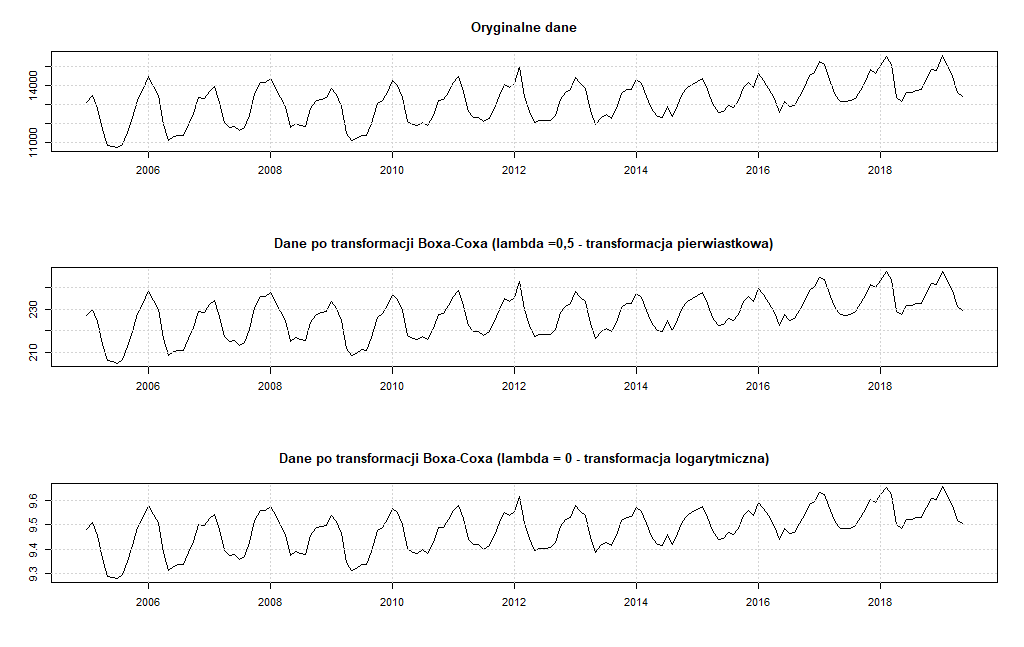
Tak jak można było przypuszczać, nie widać istotnych różnic pomiędzy oryginalnym a przekształconym szeregiem. Zatem dla naszego szeregu czasowego nie ma przesłanek by stosować ten rodzaj transformacji, nie zachodzi potrzeba ustabilizowania wariancji szeregu. Pozostaje różnicowanie. Różnicowanie polega na zastąpieniu oryginalnych danych szeregiem różnic wyznaczonych dla ustalonych opóźnień czasowych. Podstawową wersją operacji różnicowania jest różnicowanie z opóźnieniem 1, czyli dla kolejnych następujących po sobie wartościach. W naszym przypadku mamy efekt sezonowości rocznej, czyli zastosujemy najpierw różnicowanie z opóźnieniem sezonowym wynoszącym 12.
# różnicowanie z opóźnieniem 12
zuzycie.ts.adj.diff12 <- diff(zuzycie.ts.adj, 12)
Pokażmy wynik tego działania:
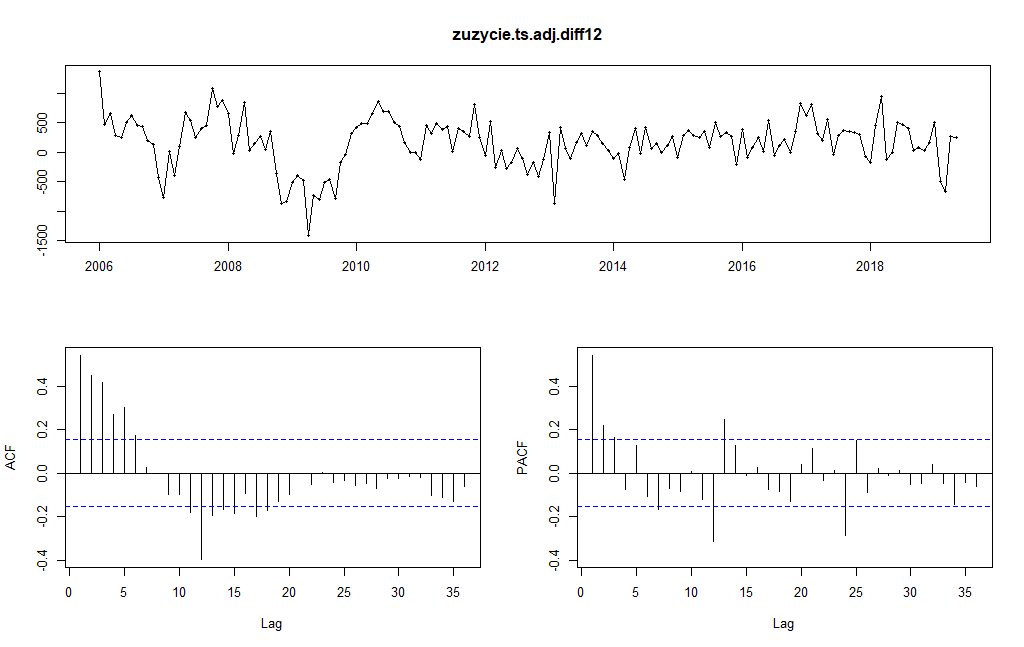
Czy usunięta została sezonowość? Czy usunięty został trend? Tak zdecydowanie usunięte zostały efekty sezonowe, i praktycznie został wyeliminowany trend długoterminowy. Aby przekształcony szereg był jeszcze bardziej zbliżony do szeregu stacjonarnego można na nim jeszcze raz przeprowadzić operację różnicowania, tym razem z okresem 1. W wyniku tej operacji mamy:
# różnicowanie z opóźnieniem 1
zuzycie.ts.adj.diff12.diff1 <- diff(zuzycie.ts.adj.diff12,1)
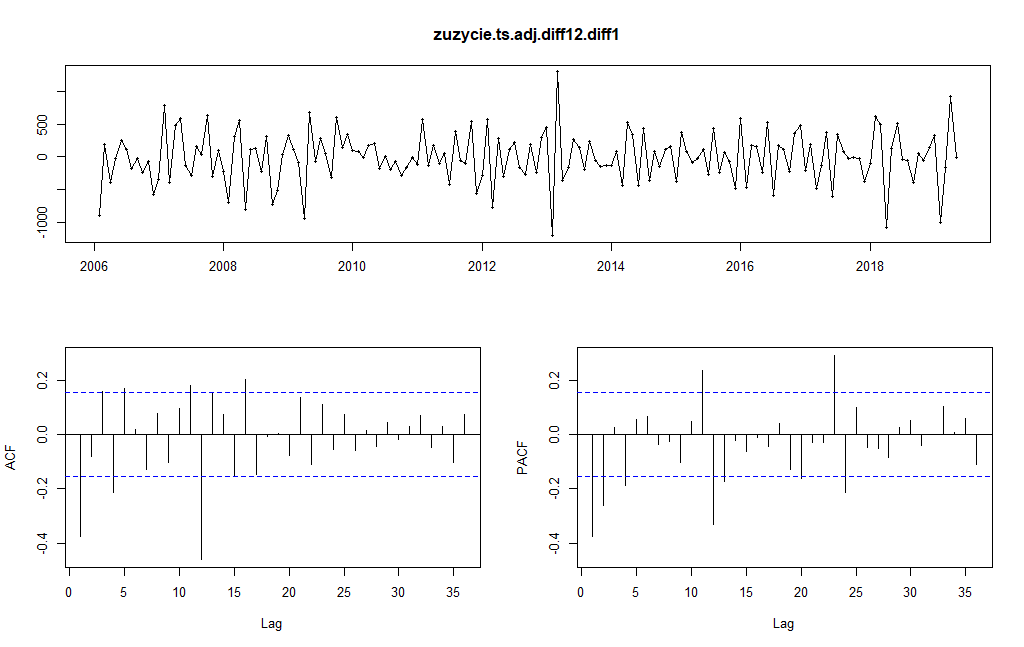
Tak przekształcony szereg można uznać za stacjonarny. Nie ma w nim regularnych składowych, a funkcja autokorelacji o niewielkich wartościach w przedziale ufności w miarę szybko zanika. Dla tak przygotowanego szeregu możemy przystąpić do identyfikacji konkretnego modelu. Model ruchomej średniej MA(q) to najprostszy model stacjonarny, który można zidentyfikować na podstawie własności funkcji autokorelacji ACF. Ostatnia istotna autokorelacja występuje dla opóźnienia h = 12. Stąd dla naszego szeregu odpowiednim mógłby być model MA(12). Z kolei dla modelu autoregresji AR(p) funkcja częściowej autokorelacji spełnia podobną rolę co funkcja autokorelacji dla MA(q). Stąd dla naszego szeregu zużycia energii elektrycznej odpowiedni byłby model AR(24). Oznacza to w rezultacie, że dla wyjściowego szeregu powinniśmy dopasować modele następujące: ARIMA(24,1,0)(0,1,0)12, ARIMA(0,1,12)(0,1,0)12. Przeprowadźmy zatem prognozę wykorzystując te modele w wytyczonym horyzoncie czasowym.
model.ARIMA1 <- Arima(zuzycie_train_ts, order=c(24,1,0), seasonal = c(0,1,0))
model.ARIMA2 <- Arima(zuzycie_train_ts, order=c(0,1,12), seasonal = c(0,1,0))
zuzycie.forecast.arima1 <- forecast(model.ARIMA1, h = horyzont)
zuzycie.forecast.arima2 <- forecast(model.ARIMA2, h = horyzont)
Wyznaczone prognozy przedstawmy na wykresie i porównajmy z wartościami rzeczywistymi.
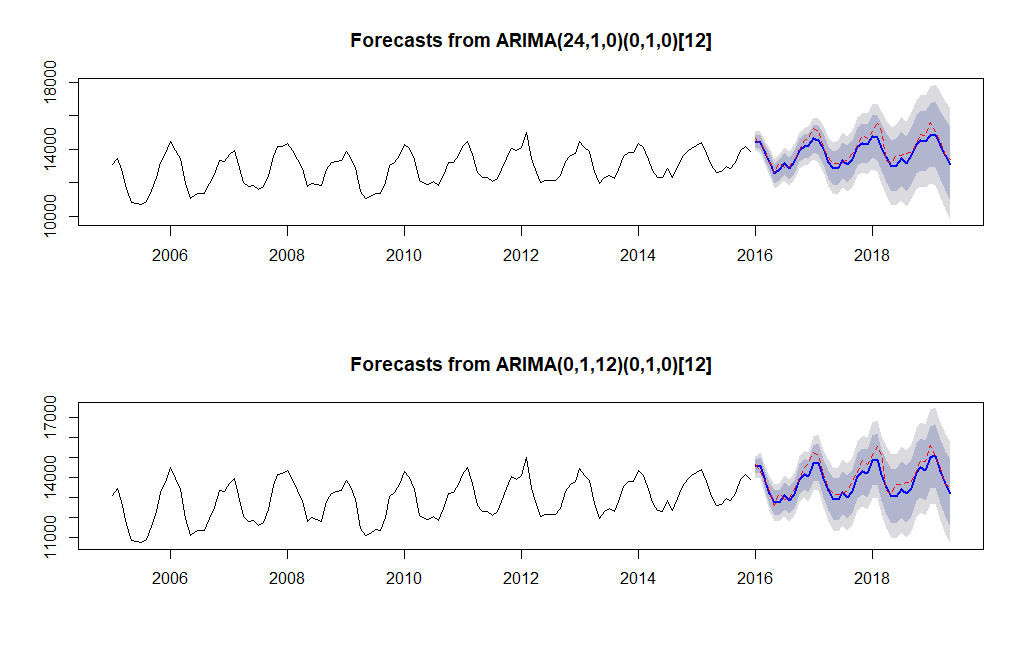
Aby łatwiej było zorientować się w wyznaczonej predykcji przedstawmy je na jednym wykresie.
ts.plot(zuzycie.forecast.arima1$mean, zuzycie.forecast.arima2$mean, zuzycie_test_ts, main="Porównanie prognoz dla obu modeli z rodziny ARIMA i wartosci rzeczywiste", col = c("red","blue","black"))
grid()
legend("topleft", legend=c("ARIMA(24,1,0)(0,1,0)","ARIMA(0,1,12)(0,1,0)","Rzeczywiste"), col = c("red","blue","black"), bg="white")
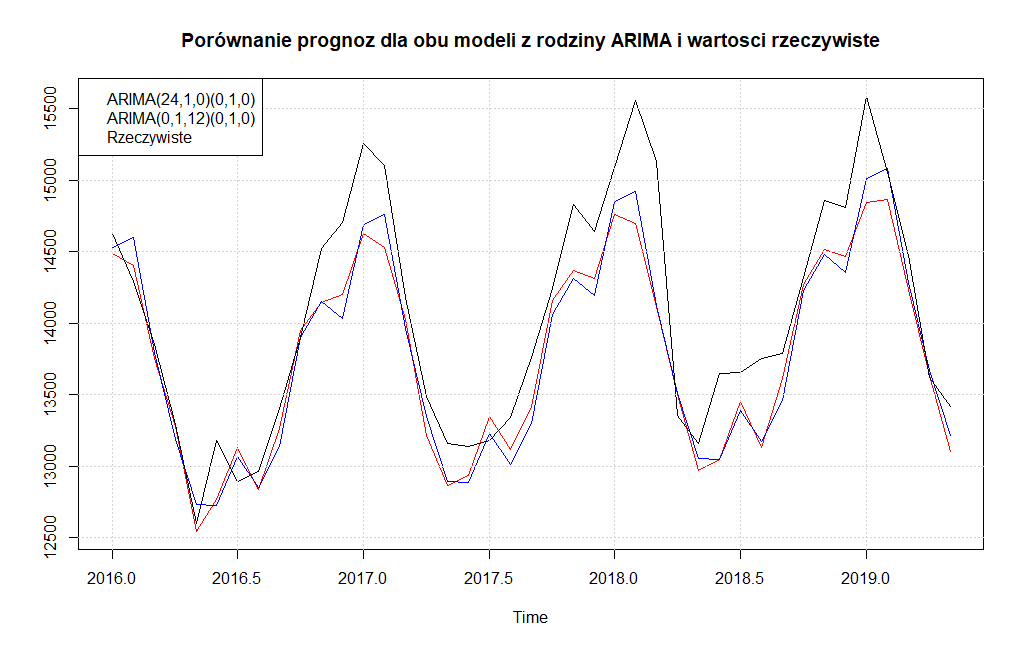
Na pierwszy rzut oka wydaje się, że bardziej optymalnym modelem jest ARIMA(0,1,12)(0,1,0). Aby się przekonać sprawdźmy jeszcze kryteria błędów predykcji korzystając z funkcji accuracy().
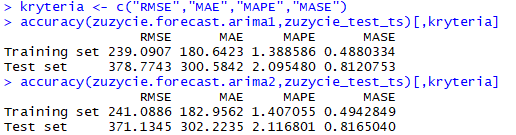
Jak widać pomiędzy kryteriami dokładności prognoz dla danych testowych nie ma znaczących różnic, aczkolwiek korzystniej wypada model ARIMA(24,1,0)(0,1,0)12.
W bibliotece forecast mamy jeszcze jedną ciekawą funkcję. Funkcja auto.arima(), bo o niej mowa pozwala zautomatyzować proces konstrukcji prognoz opartych na modelach ARIMA. Spróbujmy ją zatem wykorzystać i porównać wynik z wcześniej wyznaczonymi modelami ARIMA.
model.ARIMA3 <- auto.arima(zuzycie_train_ts)
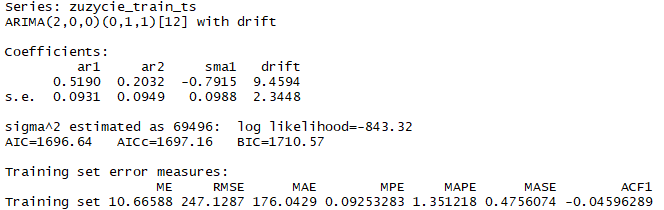
summary(model.ARIMA3)
tsdiag(model.ARIMA3)
Wyznaczony został model ARIMA(2,0,0)(0,1,1)12. Kryteria informacyjne AIC, AICC, BIC są o przysłowiowe „ciut” niższe niż dla modeli wyznaczonych ręcznie. Wykresy diagnostyczne potwierdzają poprawność dopasowania modelu do szeregu, gdyż reszty z modelu można uznać za losowe co obrazuje poniższy wykres.
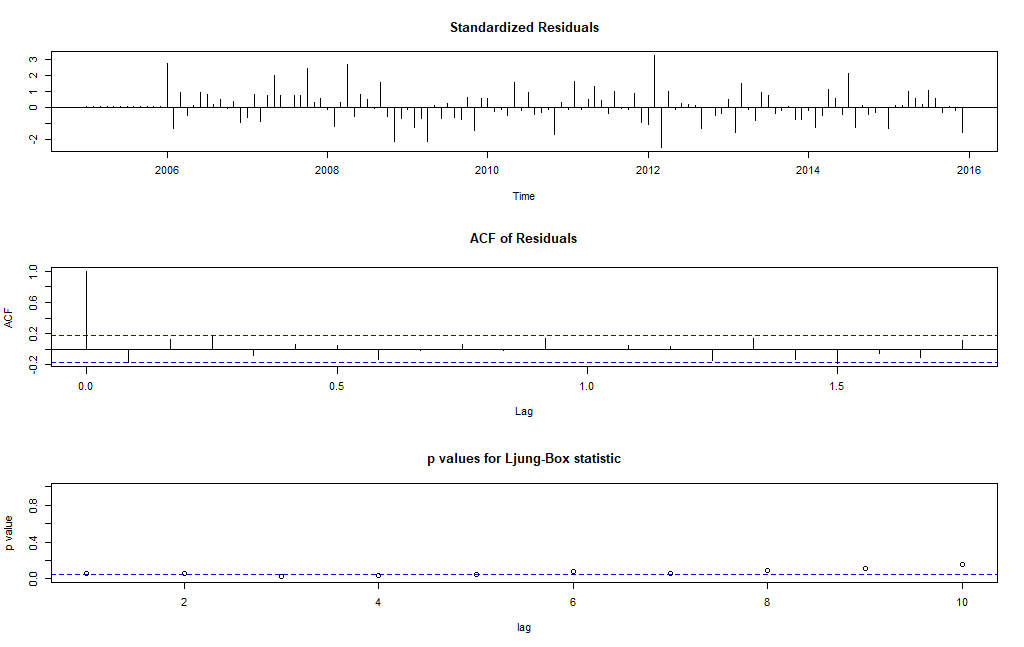
Spróbujmy zatem dla modelu ARIMA(2,0,0)x(0,1,1)[12] przeprowadzić prognozę i porównać ją z wartościami rzeczywistymi w wyznaczonym horyzoncie czasowym. Prognoza nakreślona według automatycznego modelu ARIMA została wykreślona w kolorze zielonym, a pod wykresem określono kryteria dokładności tej prognozy.
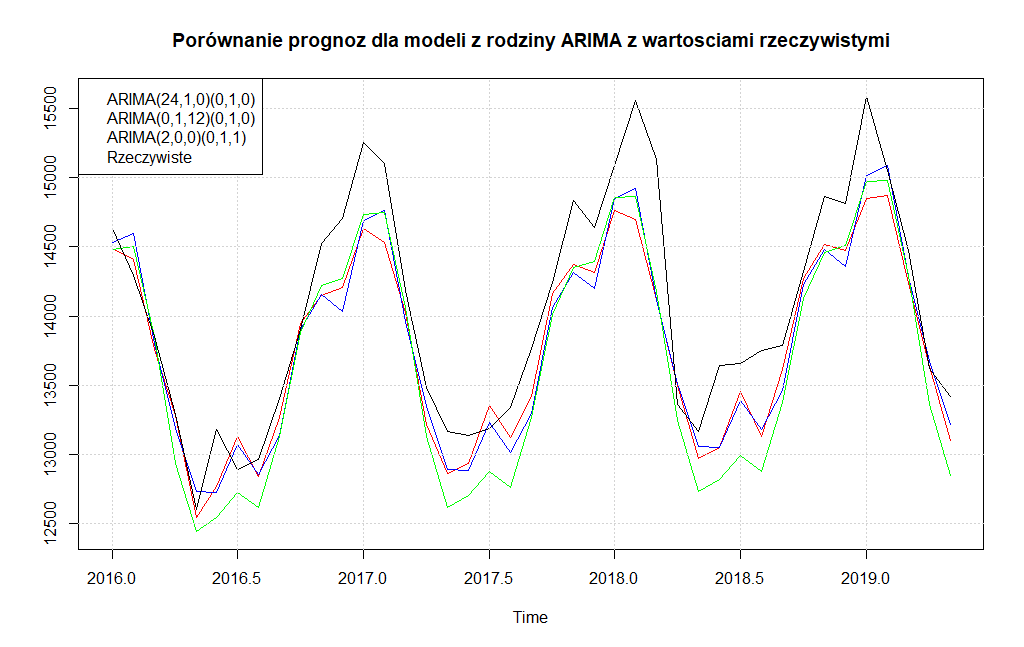

4. Prognoza oparta na metodzie naiwnej
Przedstawione powyżej rodziny metod prognozowania szeregów czasowych zostały zbudowane w oparciu o wiedzę wykorzystującą techniki statystyki matematycznej. Nie mniej jednak często spotykamy się z sytuacją, gdzie intuicja czy doświadczenie osób konstruujących prognozy pozwala na uzyskanie zadziwiająco dobrego rezultatu. Takie metody często traktuje się jako metody referencyjne, a ich wyniki stanowią zazwyczaj benchmark dla metod zaawansowanych. Do tej grupy należy między innymi metoda naiwna. W metodzie tej przyjmujemy, że wybrana historyczna obserwacja stanowi najlepszą prognozę dla przyszłej wartości szeregu czasowego. Zatem w najprostszym wariancie metody naiwnej przyjmuje się że prognoza w chwili t równa jest obserwacji w chwili t-1. A przy metodzie naiwnej sezonowej jako wartość prognozowaną przyjmuje się wartość z sezonowym opóźnieniem. Przeprowadźmy zatem prognozę stosując metodą naiwną sezonową dla naszego szeregu zużycia energii elektrycznej. W tym celu wykorzystamy funkcję snaive() z pakietu forecast.
zuzycie.forecast.snaive <- snaive(zuzycie_train_ts, h = horyzont)
Po wykreśleniu mamy:
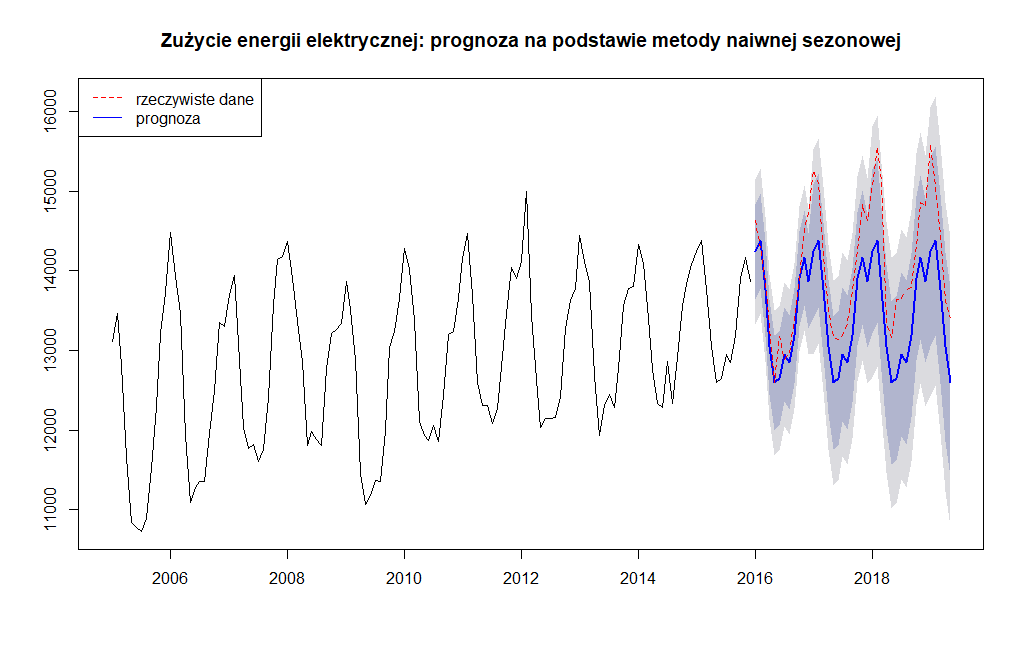
Jak widać efekt nie jest zadawalający. Mamy dość wyraźne rozjechanie się pomiędzy wartościami rzeczywistymi a prognozowanymi. Nie mniej jednak tak jak zaznaczyłem na początku metodę naiwną można traktować jako odniesienie dla bardziej skomplikowanych modeli.
5. Podsumowanie dopasowania modelu
Podsumujmy zatem dobór optymalnego modelu do naszego szeregu czasowego zestawiając w jednym miejscu kryteria błędów predykcji zgodnie z kolejnością modeli, jakie były wyżej we wpisie przedstawione. Zatem:
kryteria <- c("RMSE","MAE","MAPE","MASE")
accuracy(zuzycie.forecast.tslm, zuzycie_test_ts)[, kryteria]
accuracy(zuzycie.forecast.ets,zuzycie_test_ts)[,kryteria]
accuracy(zuzycie.forecast.arima1,zuzycie_test_ts)[,kryteria]
accuracy(zuzycie.forecast.arima2,zuzycie_test_ts)[,kryteria]
accuracy(zuzycie.forecast.arima3,zuzycie_test_ts)[,kryteria]
accuracy(zuzycie.forecast.snaive,zuzycie_test_ts)[,kryteria]
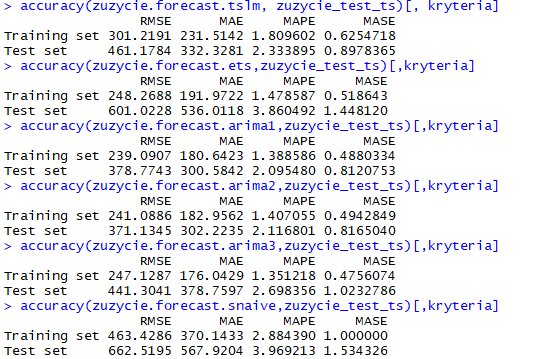
Najlepszym modelem predykcyjnym okazał się ręcznie określony model ARIMA(24,1,0)(0,1,0)[12]. Model ten powinien prowadzić do bardziej dokładnych prognoz niż np. model, który został określony automatycznie przy uwzględnieniu.
Pora na prognozę
I doszliśmy prawie do końca. Wybraliśmy najlepszy z możliwych modeli predykcyjnych dla szeregu czasowego zużycia energii elektrycznej, zatem zastosujemy teraz go do prognozy zużycia energii elektrycznej w okresie następnych 12 i 24 miesięcy
horyzont_krotki <- 12
horyzont_dlugi <- 24
model.ARIMA <- Arima(zuzycie.ts.adj,
order = c(24,1,0),
season=c(0,1,0))
ARIMA.forecast.12 <- forecast(model.ARIMA, h = horyzont_krotki)
ARIMA.forecast.24 <- forecast(model.ARIMA, h = horyzont_dlugi)
Prognoza 12-miesięczna
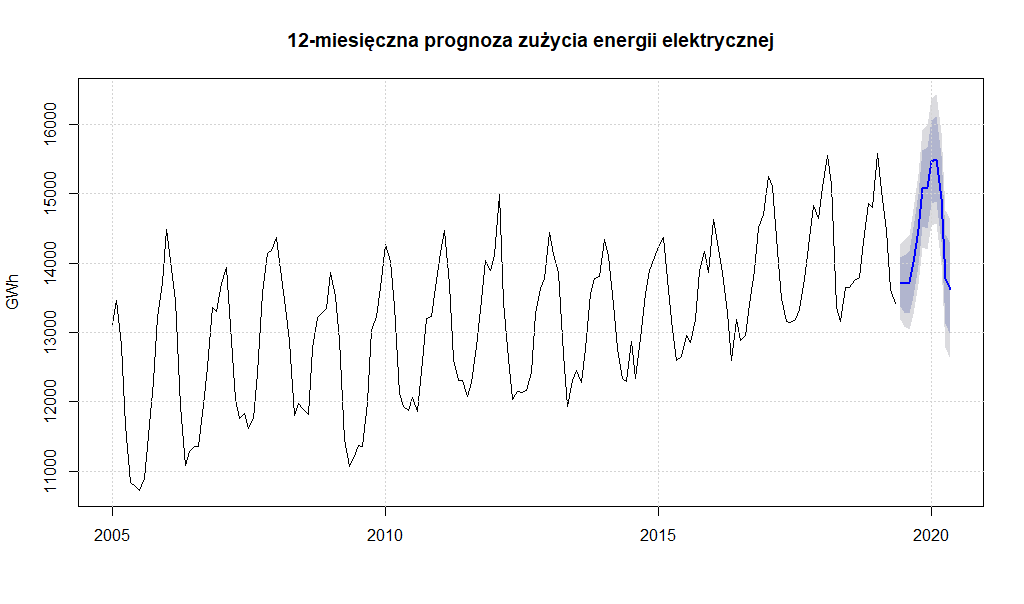
Prognoza 24-miesięczna
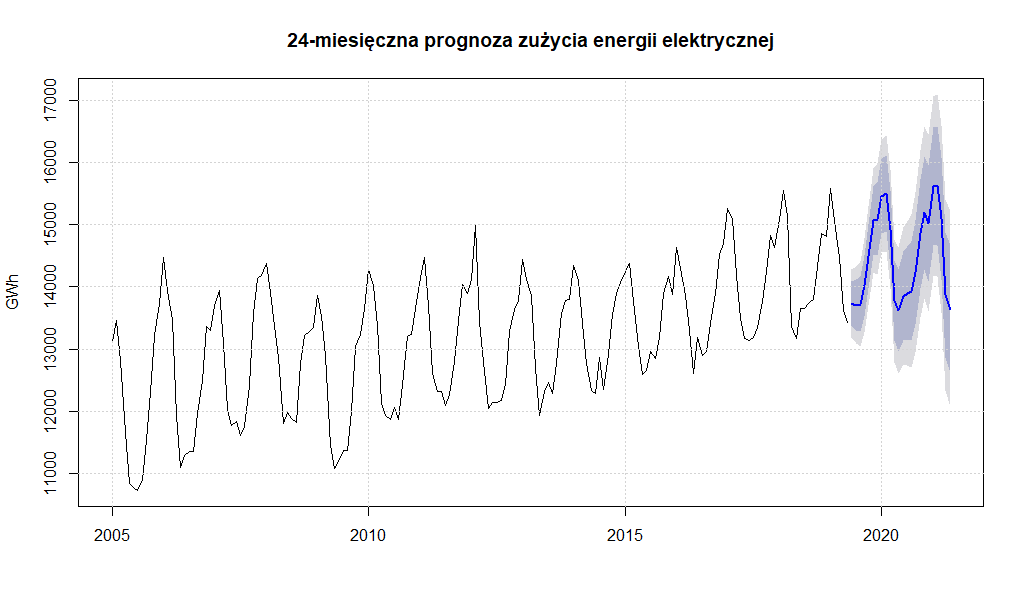
A jak będzie sprawdzimy za rok, a potem za dwa ?. Oczywiście w podobny sposób można pobawić się z szeregiem czasowym dotyczącym produkcji energii elektrycznej w elektrowniach krajowych jak również poddać prognozie saldo wymiany międzynarodowej. Płyną z tego ciekawe wnioski, zatem do dzieła i prognozujcie.





