Czy przed stosowaniem modeli uczenia maszynowego dane powinny zostać odpowiednio przekształcone, przetransformowane zgodnie z tytułem uczenie maszynowe matematyczna transformacja danych. Odpowiedź brzmi, nie jest to konieczne (aczkolwiek przy szeregach czasowych, odpowiedź może skłaniać się bardziej w kierunku konieczne 😉). To po co sobie zawracać tym głowę. A dlatego, że po pierwsze odpowiednie przetransformowanie danych może zwiększyć wydajność naszych modeli, a po drugie stosując modele liniowe, w tym logiczną regresję przyjmuje się, że zmienna ma rozkład normalny. Rozkład ten, zwany często rozkładem Gaussa jest jednym z najważniejszych rozkładów prawdopodobieństwa w statystyce. A wykres funkcji gęstości prawdopodobieństwa tego rozkładu jest dobrze rozpoznawaną krzywą dzwonową z określonymi parametrami. Jak ktoś chciałby sobie przypomnieć co to za parametry i jakimi właściwościami rozkład normalny się charakteryzuje to esencję można znaleźć we wpisie: Why is Gaussian the King of all distributions?
Dla przypomnienia, w tej serii wpisów opublikowano już:
- Uczenie maszynowe: przygotowanie danych – wprowadzenie
- Uczenie maszynowe: przygotowanie danych – brakujące dane
- Uczenie maszynowe: przygotowanie danych – kodowanie zmiennych kategorialnych
Zatem realizując któryś z wspomnianych wyżej modeli warto sprawdzić właśnie to, czy mamy do czynienia z rozkład normalnym naszych zmiennych. Metod sprawdzenia jest dość sporo poczynając od graficznych przedstawiających histogram zmiennych, wykres kwantyl-kwantyl (ang. Q-Q plot) aż po szeroką gamę testów statystycznych, z których najbardziej znane są testy Kołmogorowa-Smirnova dla prób ilościowo dużych i Shapiro-Wilka dla prób ilościowo małych. I jeżeli w wyniku przeprowadzonych testów okaże się, że rozkład zmiennej odbiega od rozkładu normalnego będąc jego asymetryczną wersją wówczas możliwym staje się zastosowanie pewnych matematycznych przekształceń, które w rezultacie zbliżają rozkład zmiennej do jej rozkładu normalnego.
Matematyczna transformacja danych
Do najczęściej stosowanych metod matematycznych przekształceń zaliczamy (po średniku podano ograniczenie metody):
- transformację odwrotną ( 1/x ; dla x != 0)
- transformację pierwiastkową ( x**(1/2) ; dla x>0 )
- transformację wykładniczą ( x**lambda)
- transformację logarytmiczną ( np.log(x) ; dla x > 0)
- transformację Boxa-Coxa ( ; dla x > 0 )
- transformację Yeo-Johnsona
W sieci można znaleźć szereg różnych stron poświęconych tym transformacjom także nie będę ich tutaj opisywał. Najbardziej złożonymi transformacjami są oczywiście dwie ostatnie, czyli Box-Cox oraz Yeo-Johnson. Szczegółowe wzory obu podane są także w dokumentacji scikit-learn.
Dane do analizy
Tak jak w poprzednich wpisach pracować będziemy na danych pochodzących ze zbioru opisującego nieruchomości House Prices – Advanced Regression Techniques. Link do zbioru danych [1].
Do transformacji przystąp
Zatem do dzieła. Tradycyjnie skorzystam z metod zawartych w pakiecie scikit-learn pamiętając o tym, że metody w wyniku zwracają transformację w postaci tablicy NumPy. Ponadto w przypadku metod Box-Cox i Yeo-Johnson transformacja uczy się swoich parametrów z danych, zatem nie zapomnijmy wcześniej podzielić zbiór na uczący i testowy przed wykonaniem transformacji.
W module preprocessing pakietu scikit-learn znajdujemy metody:
- FunctionTransformer – https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.FunctionTransformer.html#sklearn.preprocessing.FunctionTransformer
- PowerTransformer – https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html#sklearn.preprocessing.PowerTransformer
Z uwagi na to, ze poszczególne matematyczne metody transformacji mają swoje ograniczenia (zawarłem je wyżej przy wymienieniu metod) to z dostępnej puli zmiennych wybierzemy te zmienne, które są numeryczne i dodatnie. Następnie dla nich z grubsza wyświetlimy histogramy celem szacunkowej oceny rozkładu zmiennej.
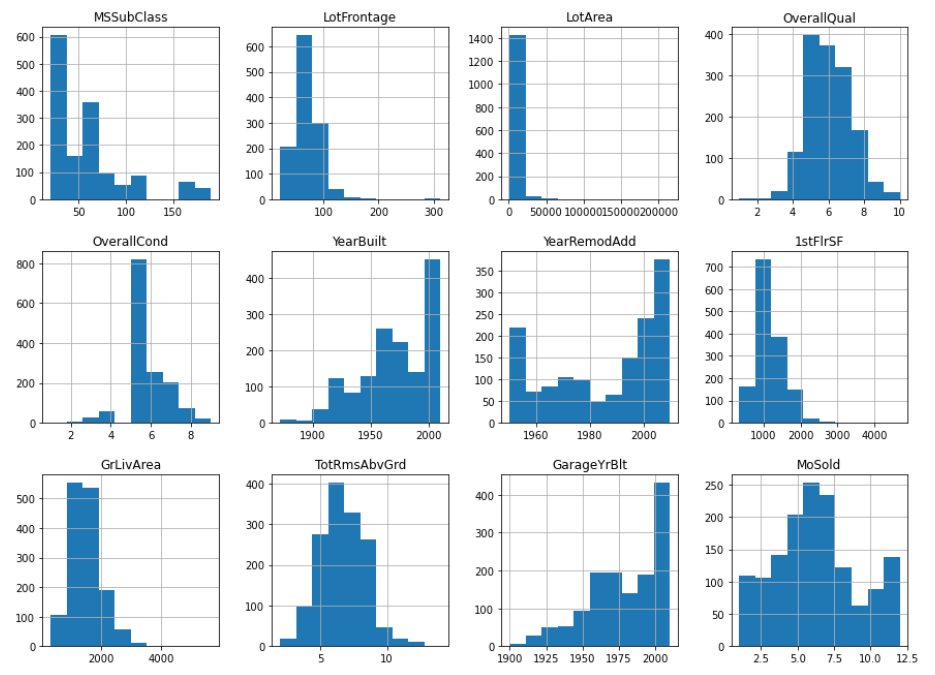
Z kolei pełniejsza ocena rozkładu zmiennej przed i po transformacji zostanie dokonana na podstawie histogramu oraz wykresu Q-Q plot.
Ładujemy odpowiednie klasy i przetestujemy transformacje dla wybranej zmiennej
Transformacja odwrotna
W pierwszym wierszu przypominana będzie oryginalna zmienna YearBuilt, w drugim z kolei zmienna przetransformowana.
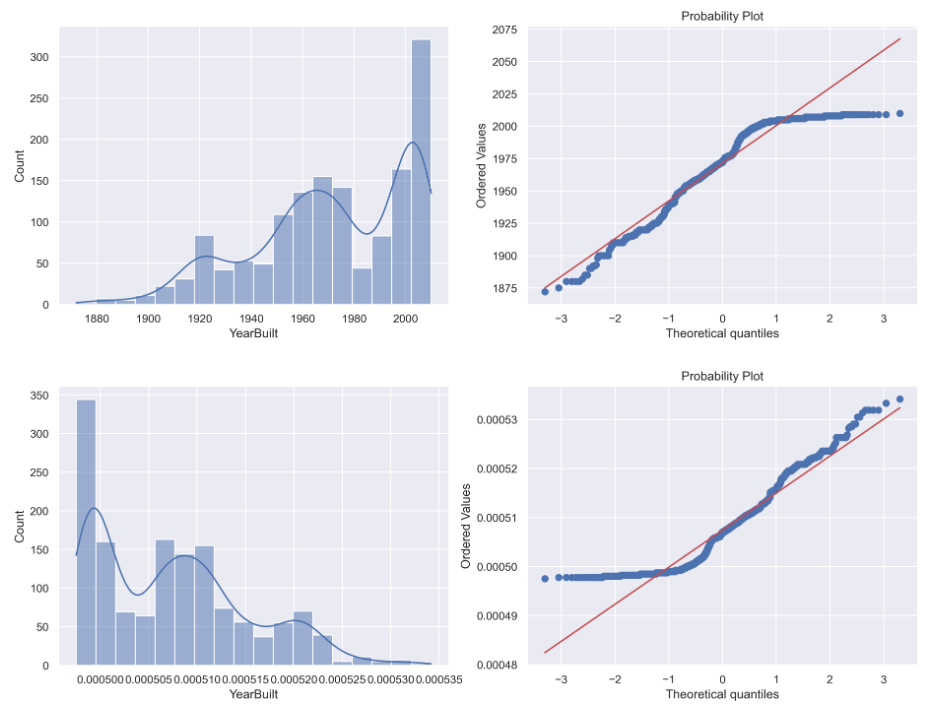
Transformacja pierwiastkowa
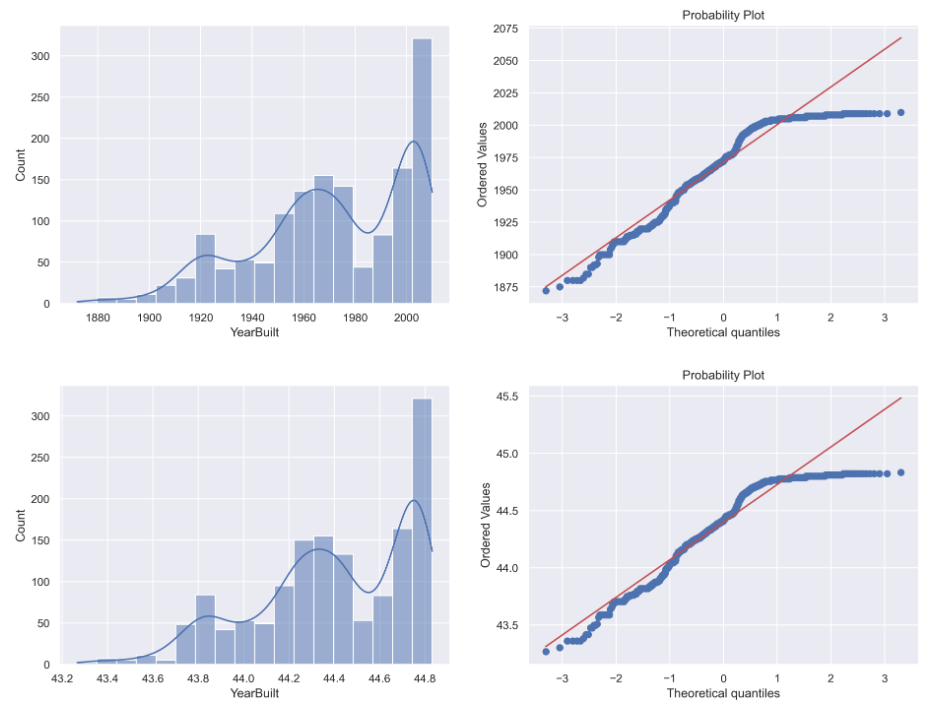
Transformacja wykładnicza
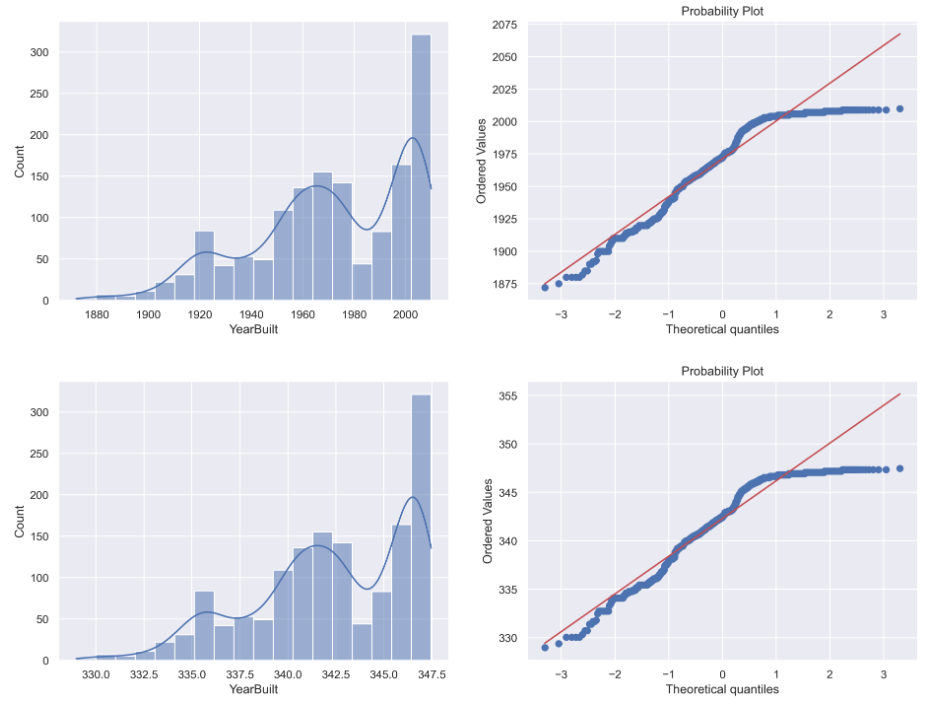
Transformacja logarytmiczna
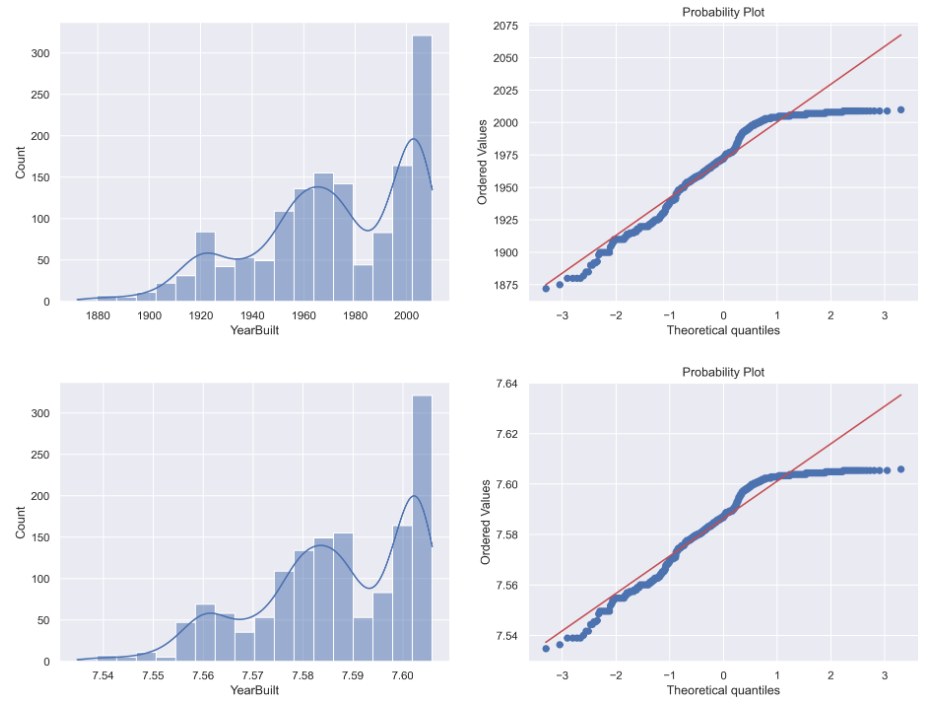
Transformacja Box-Cox
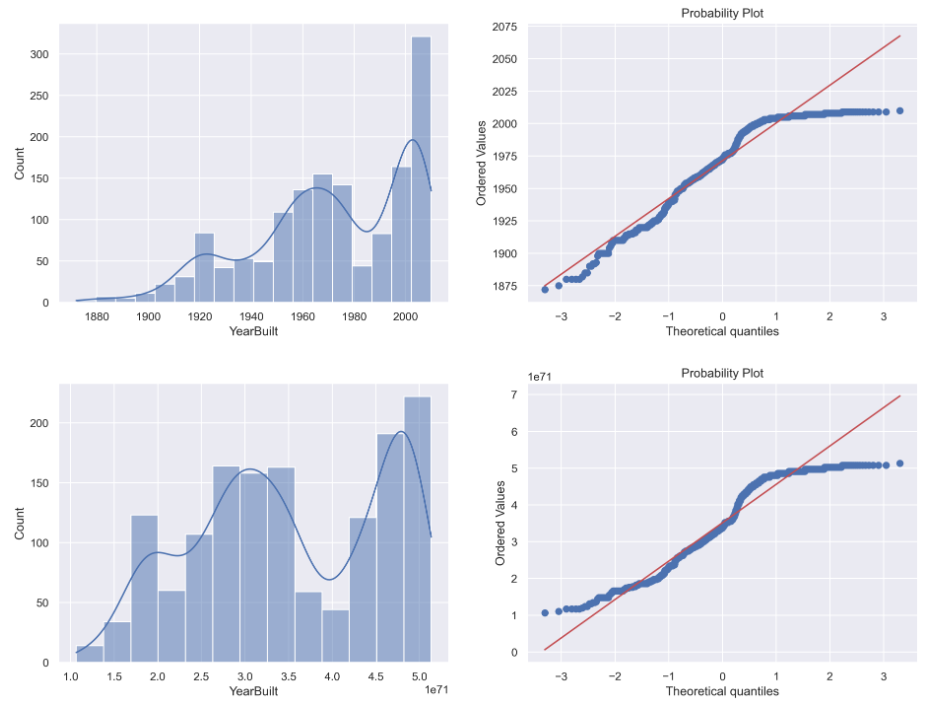
Transformacja Yeo-Johnson
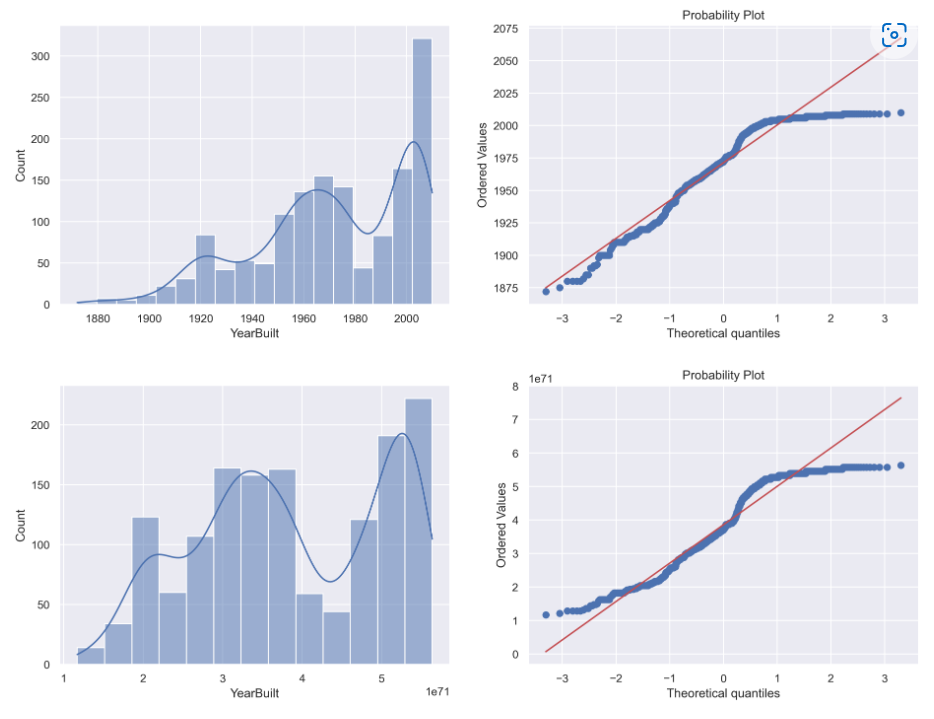
Przyglądając się poszczególnym wykresom ciężko uznać by, któraś z zaproponowanych transformacji sprawdziła się przy przekształceniu zmiennej „YearBuilt” w kierunku zmiennej o rozkładzie normalnym. Niestety nie zawsze się to udaje, ale żeby nie było tak źle poniżej zademonstruje transformację Yeo-Johnson dla innej zmiennej „1stFlrSF”.
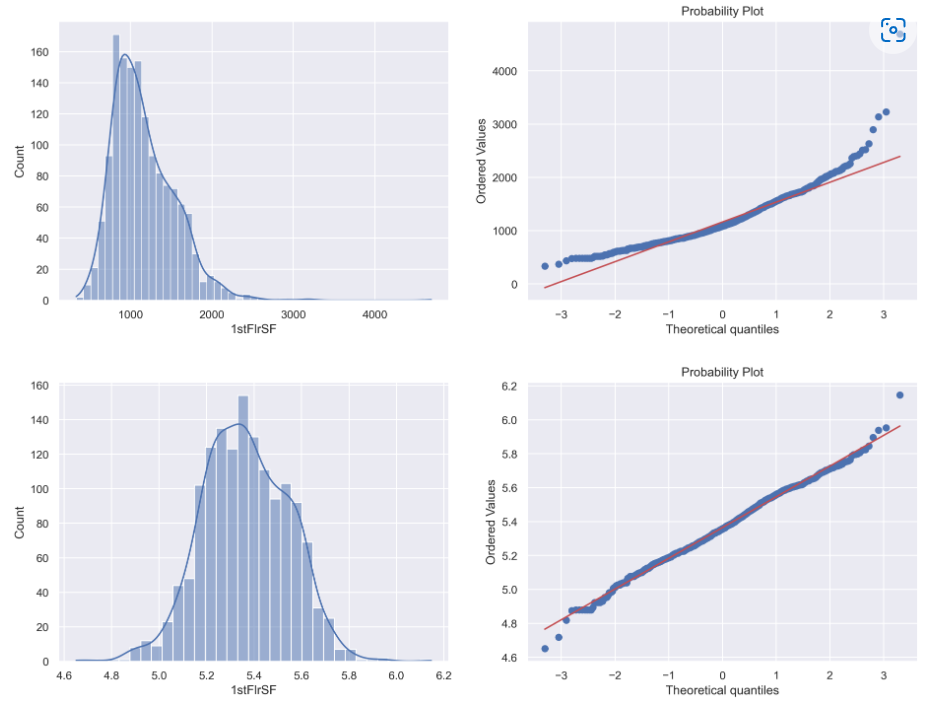
W tym przypadku może nie jest to jeszcze idealna transformacja, ale postęp z pewnością jest już znacząco zauważalny. Wśród zmiennych, dla których wyrysowano na początku histogram są i takie, gdzie transformacja przyniesie bardzo dobre rezultaty. Które to zmienne, to już zostawiam do własnego sprawdzenia 😉 .




