Zacznijmy od tego czym są obserwacje odstające. Zgodnie z definicją zawartą w wikipedia.pl obserwacja odstająca to po prostu obserwacja relatywnie odległa od pozostałych elementów próby. Innymi słowy obserwacja, posiadająca nietypową wartość zmiennej objaśniającej (niezależnej) przez co może zniekształcać nasze analizy, a co gorsza nawet naruszać założenia przyjęte pod analizy. Biorąc zatem pod uwagę problemy, jakie obserwacja odstająca może powodować pierwszym co przychodzi do głowy, zresztą naturalnym, jest wyeliminowanie jej ze zbioru danych. Ale … !!! . Usunięcie obserwacji odstającej nie zawsze jest dobrym rozwiązaniem, wręcz odwrotnie usunięcie jej będzie uzasadnione jedynie w wybranych przypadkach. Dlaczego? Dlatego, że wartości odstające mogą być źródłem informacji na temat procesu gromadzenia danych. Warto zatem przyjrzeć się temu etapowi, i sprawdzić w jaki sposób wartości odstające się pojawiają, może się powtarzają więc tak naprawdę stanowią normalną część badanego procesu.
Z cyklu artykułów o przygotowaniu danych do procesu uczenia maszynowego przygotowano:
Identyfikacja obserwacji odstających
Zacznijmy zatem od identyfikacji obserwacji odstających. O ile się nie mylę, to nie ma ścisłych reguł statystycznych by obserwację za definitywnie odstającą uznać. Owszem są natomiast pewne wytyczne a nawet testy statystyczne, ale tak naprawdę to znajomość procesu badawczego jest kluczowa. Wyobraźmy sobie bowiem, że mamy zbiór reprezentantów Polski siatkarzy przygotowujących się do mistrzostw świata 2022, i w zbiorze (do pobrania) jest informacja o wzroście poszczególnych zawodników podanym w metrach.

W przypadku Karola Kłosa popełniono błąd i przesunięto przecinek o jedno miejsce w prawo. Zobaczmy jak kształtować będzie się średnia oraz odchylenie standardowe dla przypadku gdy zostawimy lub usuniemy obserwację odstającą.
| „Z” obserwacją odstającą | „Bez” obserwacji odstającej | |
| Średnia [m] | 2,59 | 1,97 |
| Odchylenie standardowe [m] | 3,36 | 0,07 |
Z tabeli widać, jak jedna obserwacja odstająca potrafiła zniekształcić nasz zbiór. Średnia wzrostu siatkarzy wyniosłaby bowiem 2,59 [m], a odchylenie standardowe 3,36 [m]. W porównaniu do prawidłowych danych odchylenie standardowe przy danych z obserwacją odstającą wzrosło niebotycznie. Stąd wniosek, że testy hipotez, które wykorzystują średnią będą po prostu chybione. Ok, jak zatem zidentyfikować obserwację odstające w danych.
Chyba najprostszym sposobem jest posortowanie danych i spojrzenie na wartości minimalne i maksymalne. Wróćmy do naszego zbioru. Gdybyśmy go posortowali według wzrostu, to od razu zauważylibyśmy, że coś z naszym zbiorem jest nie tak. Bo raczej trudno uwierzyć by Karol Kłos mierzył 20,1 m. Innym sposobem jest podejście graficzne. W tym celu możemy skorzystać z takich rodzajów wykresów jak: wykres pudełkowy [1] (często określany jako wykres ramka-wąsy) czy histogram [2]. W analizowanym przypadku, czyli zbioru ze wzrostem siatkarzy, będzie to wyglądać następująco. Do wygenerowania wykresów skorzystałem z biblioteki seaborn. Na wykresie pudełkowym obserwacja odstająca zaznaczona jest symbolem położonym z dala od pozostałej części wykresu. Ze względu na skalę trudno nawet dostrzec, ze pozostała część wykresu to nasze „pudełko”. Po usunięciu obserwacji wątpliwości już nie ma 😉.

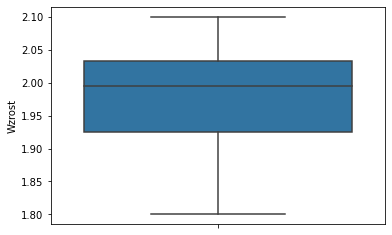
Z kolei na histogramie dostrzeżemy odizolowane słupki, tak jak w naszym przypadku gdzie obserwacja odstająca znalazła się daleko po prawej stronie od słupka pierwszego.

Przy rozkładzie normalnym zmiennej uznaje się, że jeżeli wartość obserwacji przekracza średnia ± 3 x odchylenie standardowe wówczas jest obserwacją odstającą.
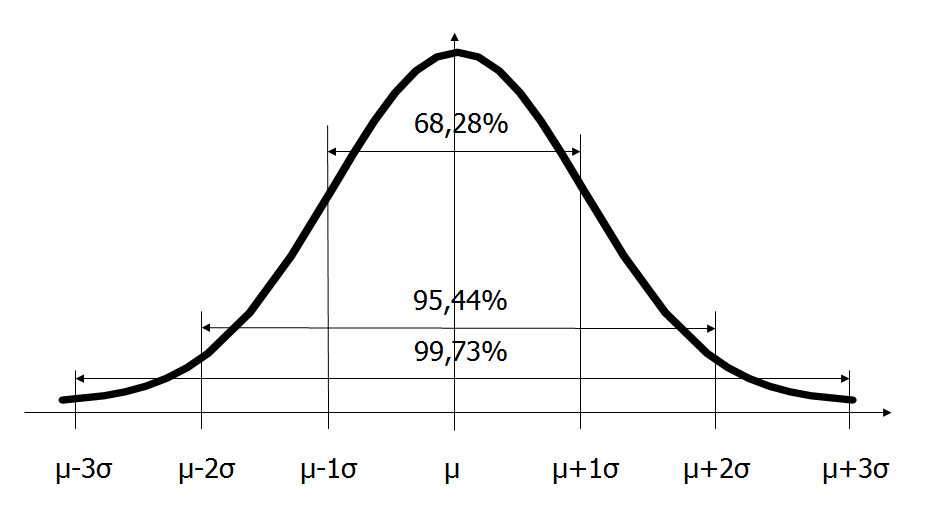
Dla rozkładu lewo lub prawoskrętnego można posłużyć się zakresem międzykwartylowym (ang. inter-quantile range IQR) mnożąc jego wartość przez 3. Obserwacje przekraczające wyznaczoną wartość uznaje się za znaczącą obserwację odstającą.
I na koniec wróćmy jeszcze do testów statystycznych pozwalających zweryfikować czy w naszym zbiorze występuje obserwacja odstająca. Jednym z takich testów jest test Grubbsa [3]. Procedura testu Grubbsa testuje hipotezę zerową (H0: sig = 0) zakładającą, że wszystkie wartości w próbie pochodzą z jednej populacji o rozkładzie normalnym, natomiast hipoteza alternatywna (H1: sig < 0) zakłada że jedna wartość nie została pobrana z tej samej populacji o rozkładzie normalnym, co inne wartości. W pakiecie outlier_utils [4] mamy metodę smirnov_grubbs. Zasada działania tej funkcji jest taka, ze obserwacja odstająca jest usuwana ze zbioru (także warto mieć to na uwadze). Indeks obserwacji odstającej jest zwracany przez metodę max_test_outlines.

Jak radzić sobie z obserwacjami odstającymi?
Wspomniałem już, że usunięcie ze zbioru obserwacji odstającej nie zawsze jest najlepszym rozwiązaniem. Zatem czy usunąć czy zostawić takie wartości zależy przede wszystkim od przyczyny, która to spowodowała. Bowiem, za wartością odstającą stać może: błędne wprowadzenie danych (jak w powyższym przypadku), błędy pomiaru, problemy z próbkowaniem w nietypowych warunkach czy wręcz naturalna skłonność do generowania takich wartości.
- Jeżeli wartość została źle wprowadzona, popełniono błąd, który jak w przypadku wzrostu naszych siatkarzy jest łatwo rozpoznawalny i można go skorygować to najlepiej to zrobić. Jeżeli nie da się skorygować to wówczas opcją jest usunięcie ponieważ wiemy, że jest to zwyczajnie nieprawidłowa wartość.
- W przypadku problemów z próbkowaniem. Wyobraźmy sobie, że ma miejsce jakieś nietypowe zachowanie, w rezultacie którego otrzymujemy wyniki, które różnią się od tych otrzymywanych w prawidłowo prowadzonym procesie. W rezultacie wyniki w tych nietypowych warunkach nie odzwierciedlają docelowej populacji. A więc na usunięcie takich wartości można przystać.
- Jeżeli mamy do czynienia z naturalną skłonnością (a gdzieś czytałem, że na około 340 obserwacji przynajmniej jedna jest nietypowa) do generowania wartości odstających to należy potraktować je jako normalną część dystrybucji danych. I lepiej wówczas zostawić taką wartość niż usuwać. Usunięcie, owszem spowoduje uzyskanie lepiej dopasowanego modelu, ale czy o to nam chodzi. Można też spróbować potraktować taką obserwację jako brakującą wartość i zastosować jedną z technik stosowanych w takim przypadku (patrz: Uczenie maszynowe: przygotowanie danych – brakujące dane )
Pamiętajmy także, że przy usuwaniu jest jeszcze jeden problem. Jeżeli obserwacje odstające są w wielu zmiennych może to doprowadzić do ograniczenia ilości danych. Ponadto przy budowaniu modeli usuwanie może mieć miejsce w przypadku zbioru uczącego, natomiast w zbiorze testowym nie powinniśmy tego robić.
Przykład
Dla zobrazowania jaki wpływ na zbiór danych może mieć usunięcie obserwacji odstających wrócę do zbioru opisującego nieruchomości House Prices – Advanced Regression Techniques. Link do zbioru danych [5].
Wybioram z niego przykładowe trzy zmienne: WoodDeckSF, TotalBsmtSF oraz GarageArea. Identyfikacja wartości odstających przedstawia się następująco:
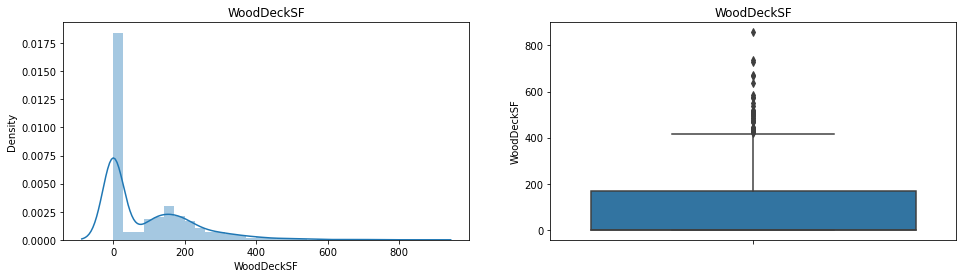
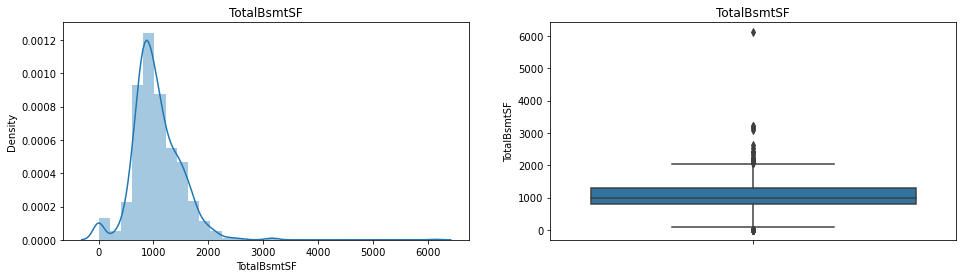
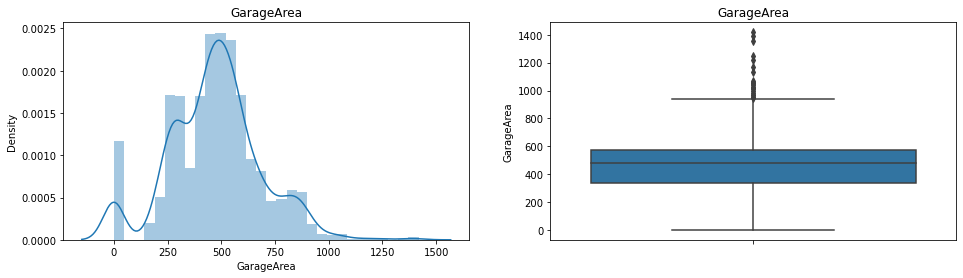
Widać, że mamy ich dość sporo. Teraz je znajdziemy. Skorzystam z identyfikacji poprzez zakres międzykwartylowy i określę dolną i górną granicę dopuszczalnego zakresu korzystając ze wzorów:
dolna_granica = Q1 – 3 * IQR
górna_granica = Q3 + 3 * IQR
Mając wyznaczone granice możemy teraz zinterpretować, które z obserwacji w zmiennych powinny być uznanae za odstające.
W rezultacie:

zostało usunięte ze zbioru osiem wierszy. Także nie jest tak źle, to nieznaczny procent w stsounku do ilości posiadanych rekordów, aczkolwiek każde usunięcie to zawsze strata informacji. Aha, jeżeli ponownie przeprowadzimy identyfikację odstających obserwacji w nowym zbiorze to ponownie możemy mieć wartości odstające. W końcu nowy zbiór to inne wartości średniej, kwartyli.



