W praktyce wielokrotnie zdarza się, że gdy zaczynamy analizować otrzymany czy też pozyskany z różnych źródeł zbiór danych okazuje się, że w wielu miejscach spotykamy się z ich brakiem. Brakujące dane w zbiorze to jeden z elementów, na który musimy zwrócić uwagę na etapie przygotowania danych (ang. data preprocessing).
Ciąg działań w uczeniu maszynowym przedstawiłem we wpisie: Uczenie maszynowe: przygotowanie danych – wprowadzenie
Brak danych może wynikać z różnych przyczyn. Mogą to być sytuacje naturalne, gdy np. ktoś odmawia udziału w badaniu, nie chce lub nie umie odpowiedzieć na zadane pytanie czy choćby podczas wyborów znane są jedynie wstępne wyniki z części komisji wyborczych. Mogą to być także sytuacje sztuczne, gdzie brak danych pojawia się po usunięciu ze zbioru obserwacji odstających (ang. outliers). Dla przypomnienia obserwacja odstająca to względnie odległa od pozostałych elementów próby, czyli wartość zmiennej o nietypowej wartości.
Tak więc braki danych stanowią element niemalże każdego zbioru danych. Czasem problem ten może być marginalny, ale w wielu sytuacjach liczba braków danych może być znacząca. Nie mniej jednak braków danych nie można ignorować. Uważa się bowiem, że występowanie braków danych w badaniu może rodzić wiele problemów począwszy od zniekształcenia rozkładów analizowanych zmiennych po zniekształcenie wyników, czy wręcz wyciągniecie błędnych wniosków z prowadzonego badania. W uczeniu maszynowym opracowany model może okazać się bezużyteczny.
Jak radzić sobie zatem z takim brakiem danych?
W tym miejscu nie sposób nie wspomnieć o pewnym artykule z odległej przeszłości 😉. W 1976 roku pojawił się krótki artykuł zatytułowany „Inference and missing data” autorstwa Donalda Rubina [1]. W nim zostały sformułowane typy mechanizmów odpowiedzialnych za generowanie braków (mechanizm całkowicie losowy MCAR, mechanizm losowy MAR, mechanizm nielosowy MNAR), a także podstawy dla obecnych technik radzenia sobie z ich brakiem w analizowanych zbiorach danych. Dlaczego te mechanizmy są tak istotne? Ponieważ od tego zależy podejście do sposobów radzenia sobie z brakiem danych. Tak to już jest, że pierwsze co przychodzi nam na myśl gdy danych nam brakuje to aby zwyczajnie je usunąć, wyeliminować ze zbioru danych.
Dla tego przypadku Rubin opracował kryterium ignorowania procesu prowadzącego do braku danych, czyli przedstawił dla jakiego mechanizmu braku danych działanie polegające na usunięciu danych ze zbioru nie będzie prowadzić do znacznych błędów w estymacji. Zainteresowanych szczegółowo tematem odsyłam do artykułu pana Rubina, a tymczasem my przyjrzymy się najczęściej stosowanym metodom radzenia sobie z brakiem danych.
Dane do analizy
Popracujemy na danych pobranych z chyba najpopularniejszej platformy do rywalizacji z zakresu uczenia maszynowego czyli Kaggle [2]. Wśród całej masy dostępnych danych tym razem skorzystam ze zbioru opisującego nieruchomości, czyli popularnego tematu oszacowania ceny z wykorzystaniem technik regresyjnych. W Kaggle zbiór można znaleźć pod hasłem House Prices – Advanced Regression Techniques [3]. Zbiór zawiera 1460 obserwacji, a zmienne zlokalizowano w 81 kolumnach.

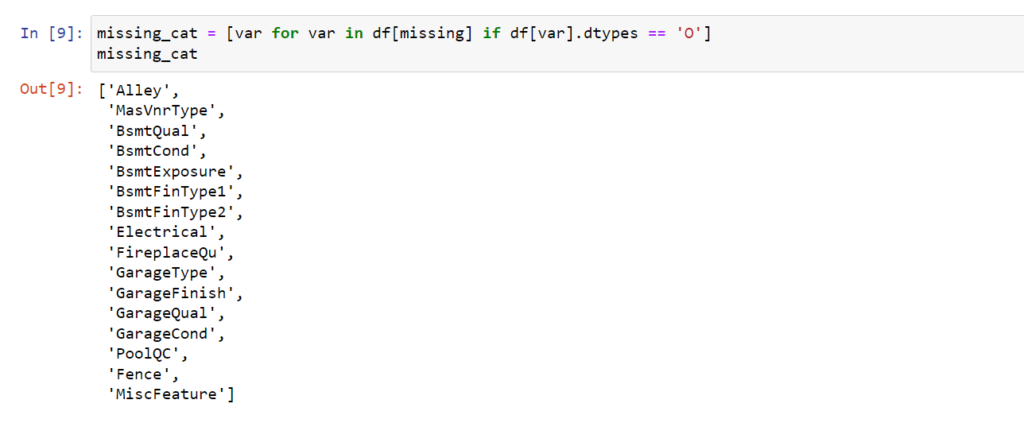
Wylistujmy te zmienne, w których mamy brak danych. Jak widać mamy 19 zmiennych w których mamy brakujące dane.
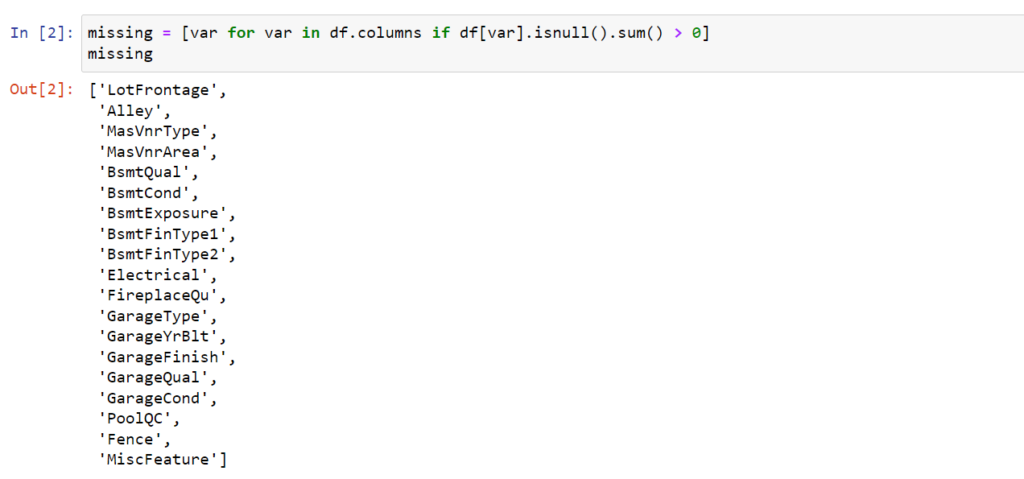
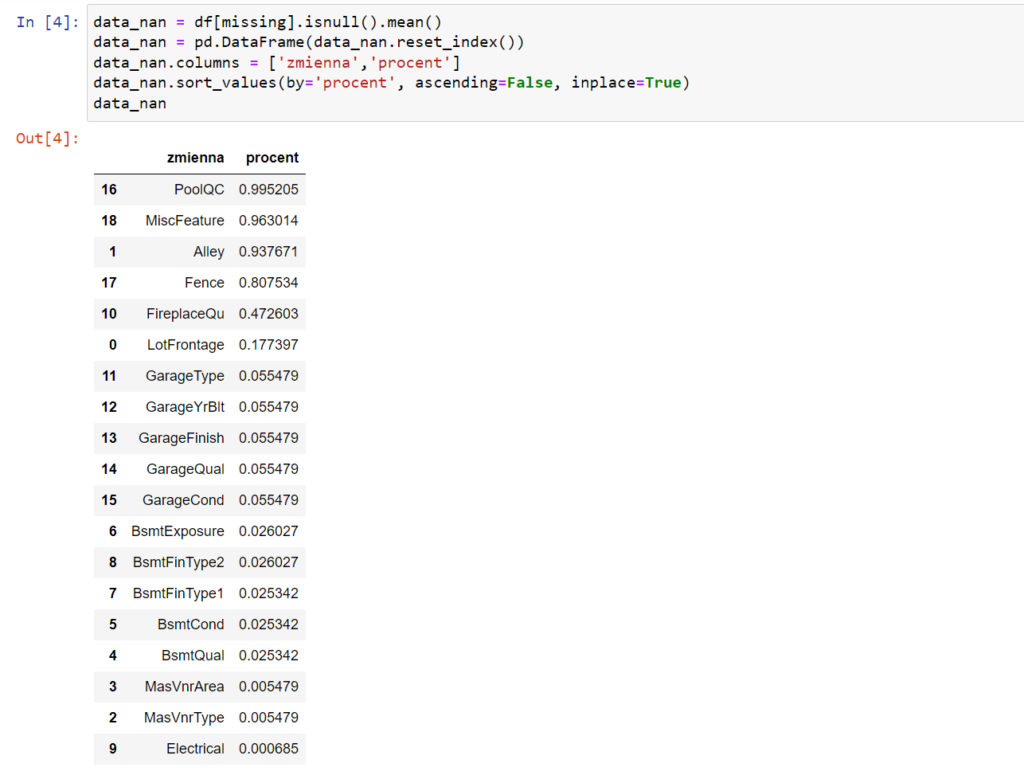
Następnie określimy procent brakujących danych dla poszczególnych zmiennych od tych z największą ilością do . Jest wśród nich dość sporo takich gdzie liczba brakujących danych przekracza 5% w ogólnej ilości. Dlaczego akurat podałem 5%, za chwilę przy omawianiu metod się okaże. Nie mniej w zbiorze mamy takie zmienne gdzie ilość brakujących danych jest bliska 100% i takie gdzie nie przekracza 0,1% (dokładnie jeden taki przypadek).
Metody radzenia sobie z brakującymi danymi
Metoda 1: usunięcie całych obserwacji w których występuje brak danych
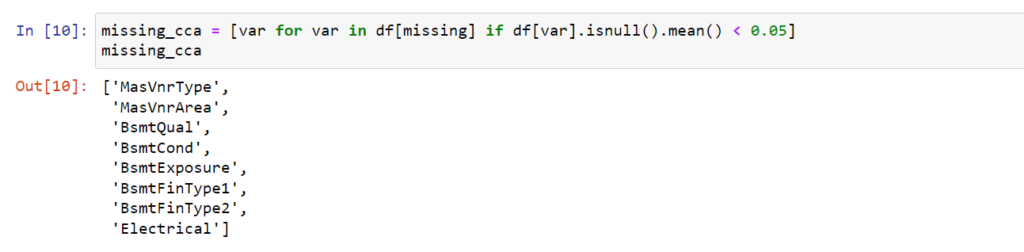
metoda ta polega na usunięciu wszystkich obserwacji gdzie występują braki danych przynajmniej dla jednej zmiennej. Często metodę określa się z angielskiego jako complete-case analysis (CCA), czyli analizie poddajemy tylko te obserwacje dla których mamy pełne dane dla wszystkich zmiennych. Metoda ta może być stosowana w mechanizmie MCAR zarówno dla zmiennych numerycznych jak i kategorycznych. Jest prosta, nie wymaga stosowania żadnych uprzednich technik manipulacji danymi. Ale musimy pamiętać o ty, że ta metoda może nas pozbawić całkiem pokaźnego zbioru obserwacji, co wpłynie na wyniki czy wręcz doprowadzi na sytuacji, że opracowany model produkcyjny może nie radzić sobie z brakującymi danymi. Także uznaje się, że metoda nie powinna być stosowana jeżeli pozbawi nas więcej niż 5% ogólnej ilości obserwacji ze zbioru.
Wyznaczmy zatem grupę zmiennych gdzie ilość braków nie przekracza 5%,
i dla tej grupy oceńmy ile obserwacji zostanie utraconych z naszego zbioru

Jest ich 48, czyli łącznie utraciliśmy niewiele ponad 3% danych. Po usunięciu tej grupy mamy do dyspozycji 1412 obserwacji. Popatrzmy zatem na rozkład, dowolnej zmiennej numerycznej, wybranej ze zbioru przed i po usunięciu obserwacji z brakującymi danymi. Rozkład nie uległ praktycznie żadnej zmianie.
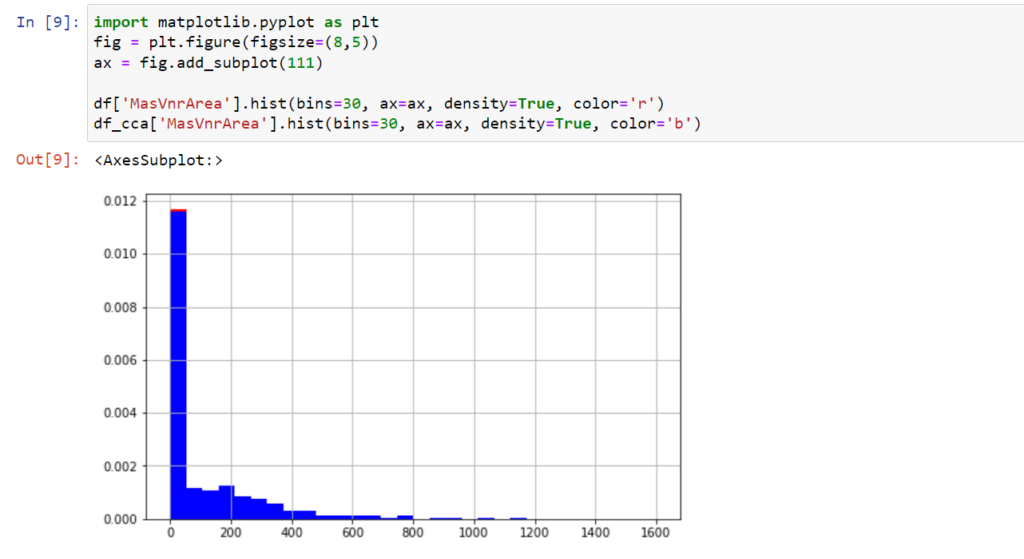
Odczucie to możemy wzmocnić obserwując funkcję gęstości.
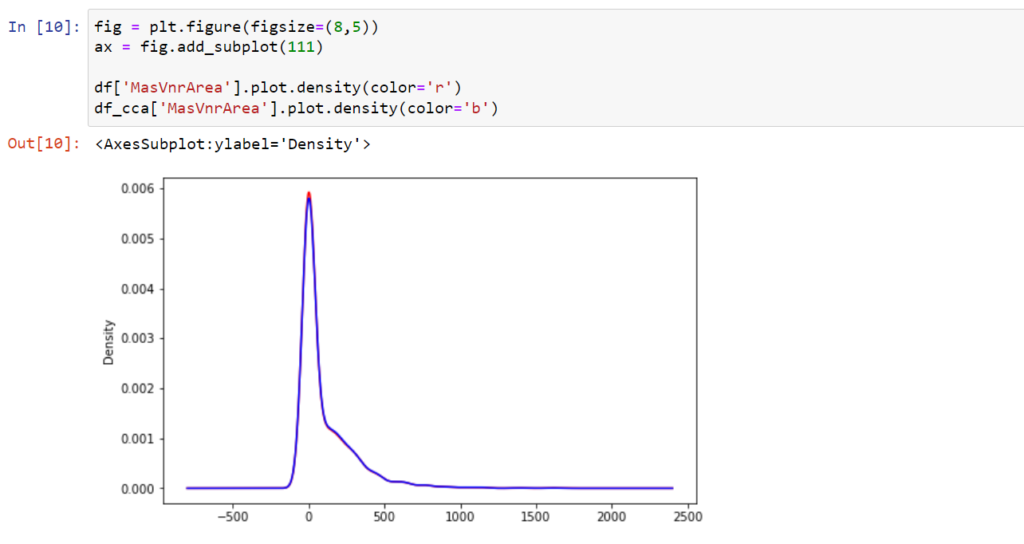
Podsumowując, w przypadku mechanizmu MCAR braki danych, o ile nie jest ich za dużo mogą być ignorowane. Dla MAR właściwości tej metody są osłabione, błędnie jest estymowana średnia choć relacje, które nie zależą od średniej pozostają nieobciążone.
Metoda 2: zastąpienie brakujących danych za pomocą wartości średniej
Alternatywą do usuwania obserwacji ze zbioru danych jest zastąpienie brakujących danych określoną wartością liczbową. Działanie takie określa się jako imputacja, i najczęściej polega na wykorzystaniu wartości średniej z próby obserwowanych wartości zmiennych.
Zatem imputację brakujących danych, w dalszej części wpisu, realizować będę z wykorzystaniem procedur udostępnionych w bibliotece scikit-learn [4], a konkretnie posłużę się metodą SimpleImputer [5]. Metoda ta dostarcza narzędzi do zastępowania brakujących danych przez wartość średnią lub medianę dla zmiennych numerycznych oraz najczęściej występującą kategorią dla zmiennych kategorycznych. Jest szybka, łatwa w stosowaniu. Mankamentem można jedynie określić konieczność przekonwertowania wyniki do postaci ramki danych, z uwagi na to że metoda zwraca tablicę tzw. numpy array.
Ok, czas przystąpić do działania. Z naszych zmiennych, w których występują braki danych wybierzemy te, które są numeryczne. Na liście mamy trzy takie zmienne. Są to 'LotFrontage’, 'MasVnrArea’ oraz 'GarageYrBlt’.

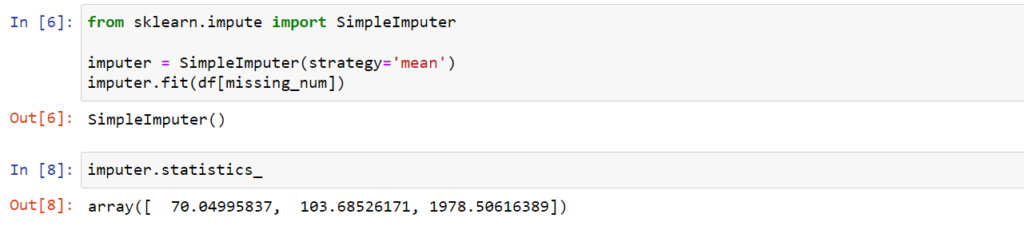
Tworzymy instancję obiektu SimpleImputer. W ramach konstruktora obiektu parametr strategy odpowiada za sposób zastąpienia brakujących danych. Zgodnie z tytułem obecnej metody skorzystamy z wartości średniej. Stąd do strategy przypiszemy wartość mean. A następnie korzystając z metody fit dopasujemy strategię do zastąpienia brakujących danych w grupie zmiennych. Wartości średnich możemy podejrzeć zaglądając wprost do atrybutu statistics_ obiektu SimpleImputer. Przedstawiono to na poniżej.
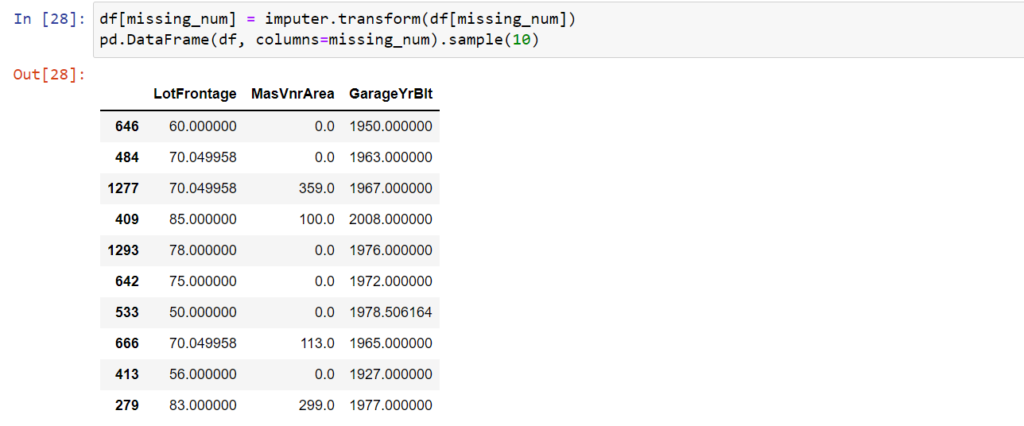
Pozostaje teraz przekształcić brakujące dane poprzez metodę transform obiektu SimpleImputer i spojrzeć na przykładową próbkę, gdzie widać, ze brakujące dane zostały zastąpione wartością średnią.
Popatrzmy jak zmieniły się histogramy zmiennych przed imputacją wartością liczbową i po jej zastosowaniu. Kolorem czerwonym zaznaczono histogram po imputacji.
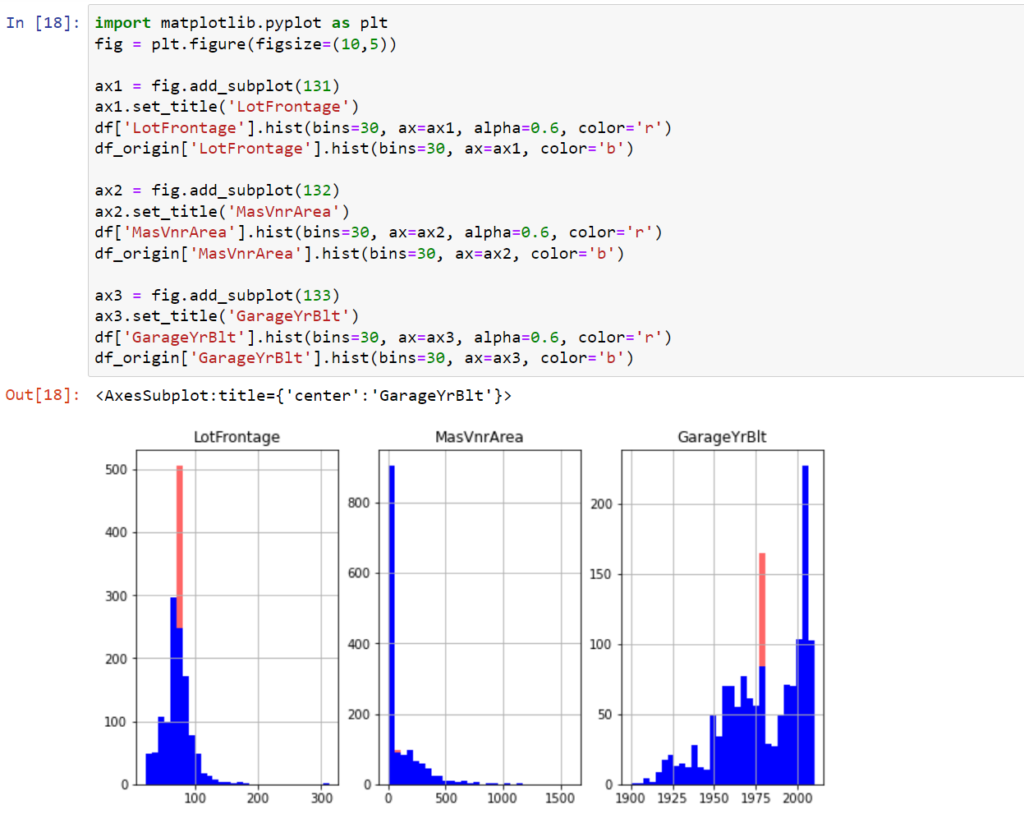
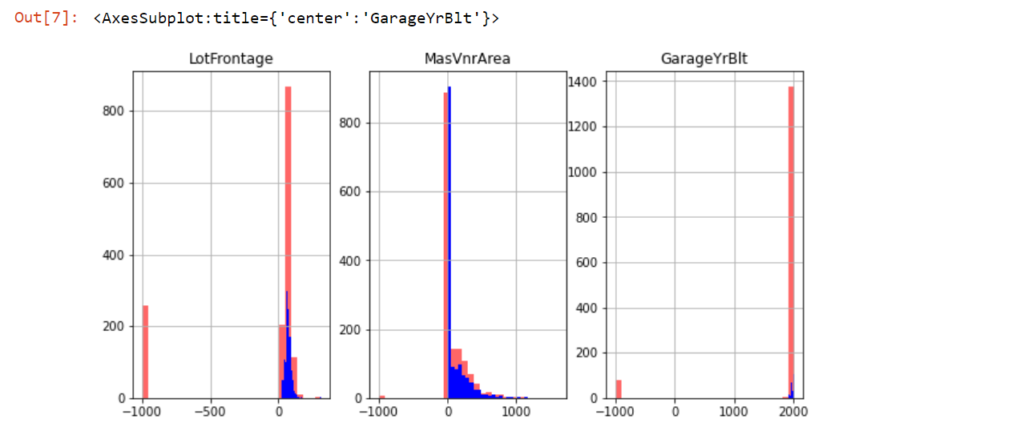
Jak widać są zmienne, w których zmiany są widoczne. To oczywiście skutek ilości brakujących zmiennych. Dla przypomnienia, w przypadku zmiennej LotFrontage zastąpionych zostało średnią ponad 17% brakujących danych, w przypadku zmiennej GarageYrBlt było to 5%, a w przypadku zmiennej MasVnrArea mniej niż 0,6%. W rezultacie zastępowania braków danych wartością liczbową (średnią) następuje zaniżenie wariancji (odchylenia standardowego) zmiennej.
Metoda 3: zastąpienie brakujących danych za pomocą dowolnej wartości
Tak jak w poprzednim przypadku brakujące dane zastępujemy dowolną wartością. Najczęściej przyjęło się przyjmować liczby ze zbioru [-999, 999], ale może to być dowolnie dobrana do naszego zbioru liczba. Korzystając z obiektu SimpleImputer postępujemy w sposób zademonstrowany powyżej. Jedyną zmianą jest w wywołaniu instancji obiektu SimpleImputer dodanie parametru fill_value oraz zmiana strategy na constant. Wygląda to zatem tak.
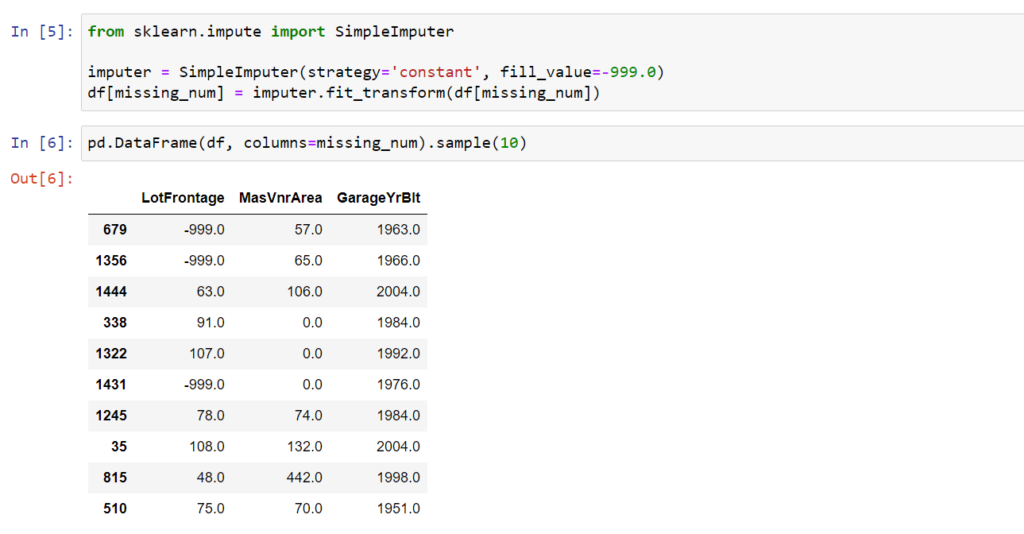
Rozkład zmiennych po imputacji dla wybranej liczby zastępującej braki przedstawia się następująco.
Metoda 4: zastąpienie brakujących danych za pomocą najczęściej występującej wartości
Metoda ma zastosowanie przede wszystkim do zmiennych kategorycznych. Stąd tez z naszego zbioru danych wybierzemy te zmienne. Mamy ich całkiem pokaźny zestaw.
Z obiektu SimpleImputer korzystamy ze zmiany strategii określając ją jako most_frequent.
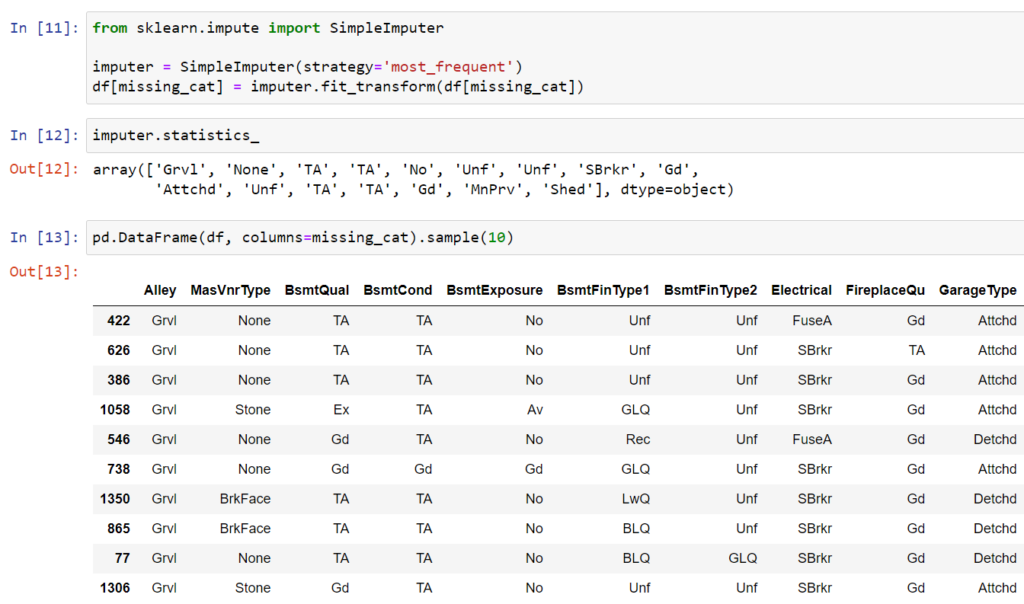
W rezultacie najczęściej pojawiające się kategorie w zmiennych zastępują w wyniku imputacji brakujące dane dla poszczególnych zmiennych.
Metoda 5: zastąpienie brakujących danych za pomocą nowej kategorii
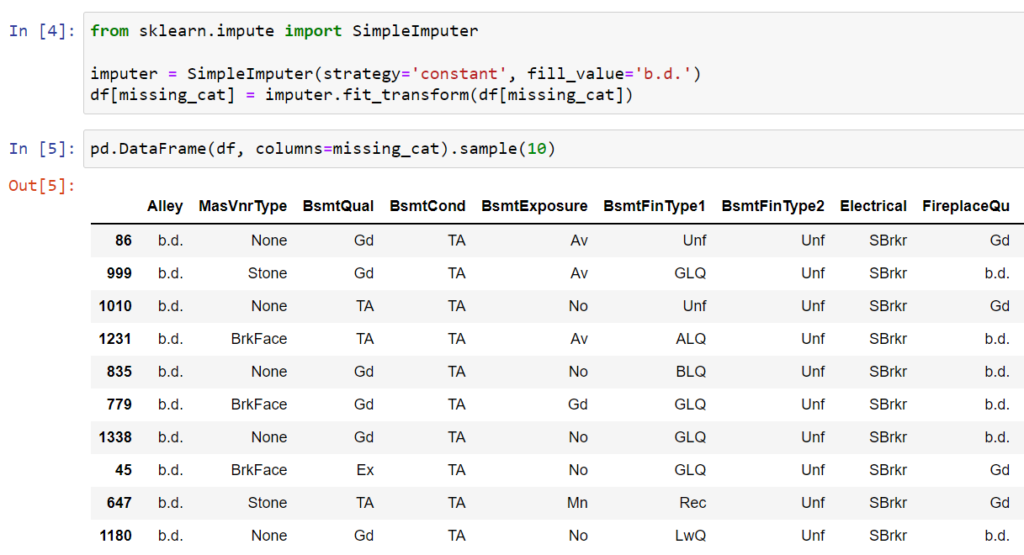
Oczywiście można także utworzyć dodatkową kategorię dla zmiennej, która dla przykładu nazwiemy skrótkowo b.d. (brak danych). Należy jednak pamiętać, ze jeżeli nie wydzielimy zmiennych kategorialnych to zastosowany obiekt SimpleImputer wykona to również na zmiennych numerycznych. Stad też w dalszym ciągu interesujemy się zmiennymi określonymi w missing_cat. Albo będziemy musieli wykorzystać obiekt ColumnTransformer do podziału zastosowania różnych metod imputacji.
Dla naszych wydzielonych zmiennych kategorialnych, jako parametr strategy wywołania obiektu SimpleImputer, określamy tym razem wartość constant, a w parametrze fill_value podajemy nazwę nowej kategorii.
Przedstawione powyżej metody to tylko niektóre z całej listy możliwych. Jako wprowadzenie do tematu niech posłuży artykuł „Wybrane statystyczne metody radzenia sobie z brakami danych” [6].
Uwaga: przy opracowywaniu modeli w uczeniu maszynowym wszelkie operacje dotyczace przygotowania danych prowadzimy na zbiorze treninigowym.




Jaki jest cel zastępowania braków dowolnymi wartościami? A zwłaszcza takimi spoza zakresu zmiennej numerycznej? W ten sposób wprowadzamy outliery, z którymi później i tak sobie trzeba znowu radzić w niektórych modelach. Czy może o to chodzi, że przy wybranych modelach możemy to stosować a przy niektórych nie, więc nie jest to metoda uniwersalna?
Nie wiem czy się dobrze rozumiemy, ale dowolne wartości w tekście postu, i tak też są rozumiane jako dowolne, to wartości określone z pewnego zbioru, w tym przypadku mowa o dwóch liczbach [-999 lub 999].
Zwyczajnie liczby te należy traktować jako kod. W trakcie analizy mogą być pomijane lub zastępowanie poprzez imputację. Zaletą niewątpliwie tej metody jest rzut oka na histogram.