Kodowanie zmiennych kategorialnych w uczeniu maszynowym

Jak już wiemy z poprzednich wpisów w uczeniu maszynowym wyróżniamy następujące rodzaje zmiennych: ilościowe, kategorialne oraz mieszane. I o ile ze zmiennymi ilościowymi (numerycznymi) modele radzą sobie dość dobrze, bo przecież w końcu operują na liczbach, to pozostałe rodzaje zmiennych dla opracowywanych modeli trzeba odpowiednio przygotować. Stąd też w obecnym wpisie kodowanie zmiennych kategorialnych będzie tematem wiodącym.

Z tej serii wpisów poświęconych przygotowaniu danych dla modeli uczenia maszynowego powstały już:

Dla przypomnienia zmienna kategorialna to taka, która pozwala na przeprowadzenie klasyfikacji serii danych za pomocą wartości związanych z określoną jakością czy kategorią. Zmienna kategorialna pozwala sklasyfikować, pogrupować w oparciu o informację jakościową, czyli najczęściej w danych spotkamy zmienną kategorialną z elementami stanowiącymi łańcuch tekstowy. I obecnie naszym zadaniem będzie kodowanie zmiennych kategorialnych do ich numerycznej reprezentacji, tak by można je uwzględnić w wielu algorytmach uczenia maszynowego.

Techniki kodowania zmiennych kategorialnych

Kodowanie zmiennej kategorialnej możemy przeprowadzić na wiele sposobów. Wraz z rozwojem technik uczenia maszynowego ta dziedzina nauki uległa również znacznemu rozwojowi [1]. Metodyka nie uległa jednak zmianie. Proces kodowania rozpoczynamy od rozpoznania charakteru zmiennej kategorialnej. Jeżeli zmienna ma charakter porządkowy to wówczas będzie można stosować metody z grupy kodowania porządkowego (ang. Ordinal Encoding, Integer Encoding). W przypadku, gdy zmienna nie ma charakteru porządkowego, i ponadto wymuszenie takiego uporządkowania nie byłoby dobrym rozwiązaniem z punktu widzenia opracowywanego modelu, stosujemy metody polegające na przekształceniu kategorii do postaci binarnego wektora (ang. One-Hot Encoding). Poniżej podano prosty przykład przekodowania zmiennej nominalnej o nazwie kolor w wektor binarny o długości 3.

Kolor
czerwony	1	0	0
zielony	0	1	0
niebieski	0	0	1

Oczywiście wprawne oko może zauważyć, że takie podejście generuje nam pewną nadmiarowość w kodowaniu i istnieje możliwość skrócenia tego ciągu binarnego. A i owszem, ale o tym później. Teraz jeszcze wspomną o zmiennej dychotomicznej, czyli takiej która przyjmuje jedynie dwie wartości. Często jako przykład tego rodzaju zmiennej podawana jest płeć. Wówczas zbiór kategorii takiej zmiennej kodujemy najczęściej jako liczby 0 i 1.

Dane do analizy

Podobnie jak poprzednio pracować będziemy na danych pochodzących ze zbioru opisującego nieruchomości House Prices – Advanced Regression Techniques. Link do zbioru danych [2]

Kodowanie typu Ordinal Encoding

Jak wspomniałem kodowanie porządkowe można uznać za naturalny sposób kodowania dla zmiennych porządkowych. W pakiecie scikit-learn w module preprocessing znajdziemy klasę OrdinalEncoder. Wybierzmy jeszcze jakąś zmienną z naszego zbioru. Na pierwszy rzut oka trudno uznać którąś ze zmiennych kategorialnych jako porządkową. Zatem pomysł będzie taki, aby wyznaczyć średnią cenę nieruchomości i powiązać ją z okolicą (zmienna Neighborhood). Obliczona średnia cena nieruchomości będzie wskaźnikiem uporządkowania lokalizacji, którą następnie właśnie przekodujemy do postaci numerycznej. Przy okazji zademonstruje kodowanie z żądanym porządkiem kodowania, gdyż OrdinalEncoder standardowo koduje kategorie tekstowe alfabetycznie. Zatem do dzieła.

Po wykonaniu kodu otrzymujemy zmienną numeryczną identyfikującą lokalizację nieruchomości w taki sposób, ze najmniejsza liczba (zero) została przypisana lokalizacji z najniższą wartością, a największa (24) lokalizacji gdzie cena nieruchomości jest najwyższa.

Kodowanie One-Hot Encoding/DummyVariable Encoding

Dla zmiennych kategorialnych bez uporządkowania kodowanie numeryczne, a więc określające relację między kategoriami może prowadzić do niewłaściwego działania uczonego modelu. Wymuszenie uporządkowania, tak jak zrobiliśmy to poprzednio też nie jest dobrym rozwiązaniem. Dla takich przypadków stosuje się kodowanie One-Hot Encoding, które w języku polskim określa się jako kodowanie „1 z n”. Istotą jest zastąpienie kategorii zmiennej poprzez ciąg binarny o długości n z jedną „1” w ciągu. Modyfikacją tego kodowania jest wykorzystanie ciągu binarnego o długości n-1, z uwagi na to że ciąg binarny o takiej długości zapewnia pełną informację o kategoriach zmiennej. Kodowanie poprzez ciąg „n-1” określony jest jako kodowanie ze ślepą zmienną (ang. Dummy Variable Encoding) i jest powszechnie zalecany przy wdrożeniach modeli uczenia maszynowego. Jednakże są przypadki, gdy n-elementowy ciąg może być zasadniejszy do użycia. Do nich należy choćby sytuacja, gdy interesuje nas wpływ pojedynczej kategorii lub budujemy modele oparte na drzewach decyzyjnych. Kodowanie One-Hot Encoding oprócz swoich zalet ma też i wady, do których należy rozszerzenie przestrzeni zmiennych przy braku dodania dodatkowych informacji. W przypadku wielu zmiennych kategorialnych czy nawet dużej ilości kategorii w zmiennej ma to znaczenie.

Do przeprowadzenia kodowania „1 z n” w naszym zbiorze danych skorzystam z pakietu scikit-learn. W module preprocessing znajdziemy klasę OneHotEncoder. Wcześniej dla uproszczenia realizacji procesu kodowania wybiorę kilka zmiennych kategorialnych z liczbą kategorii nie przekraczających liczby pięć.

W rezultacie powyższego kodu trzy zmienne zawierające następujące kategorie:

data preprocressing - kodowanie zmiennych kategorialnych

zostały przekodowane do następującej tablicy.

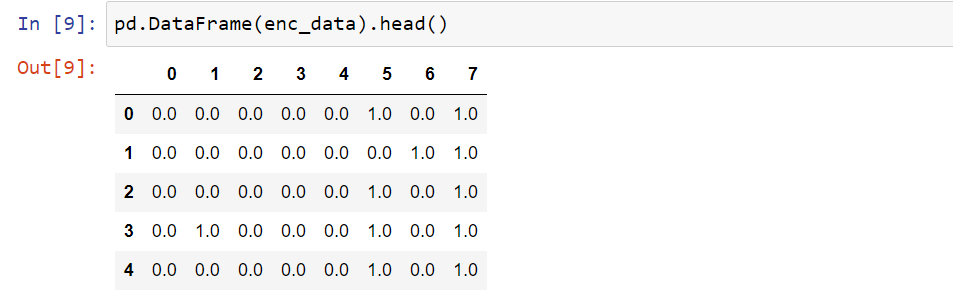
data preprocessing dummy variable encoding - kodowanie zmiennych kategorialnych

Kilka słów wyjaśnienia. W wynikowej tabeli mamy osiem kolumn, których nazwy określone zostały kolejnymi liczbami. Dlaczego jest osiem tych kolum? Dlaczego kolumny określane są liczbami całkowitymi, a nie nazwami? Dlaczego dokonałem skonwertowania wyniku do postaci ramki danych (obiekt DataFrame)? Zacznijmy od pytania pierwszego. Wpływ na to co dostajemy po przetransformowaniu obiektu klasy OneHotEncoder uzależnione jest oczywiście od parametrów, które użyliśmy do wywołania klasy. W naszym przypadku dla parametru categories przypisana została wartość auto, co oznacza, że automatycznie wszystkie kategorie będą kodowane. Ale dlaczego w wyniku mamy osiem tabel skoro wszystkich kategorii w naszych zmiennych jest jedenaście. Ma na to wpływ drugi parametr drop określony jako first. Standardowo parametr ten określony jest na None, przez co realizowane jest kodowanie One Hot Encoding (wszystkie zmienne są przekodowane). Tu użyliśmy parametru first co oznacza, że nie pierwsza kategoria w każdej zmiennej nie jest kodowana. Realizowane jest kodowanie typu Dummy Variable Encoding z ciągiem wektorowym o długości n-1. Stąd też w wynikowej tablicy, za którą odpowiada wartość False w parametrze sparce osiem kolumn. Trzy zostały usunięte (ukryte kodowanie jako wektor z samymi zerami). Również taka cecha klasy OneHotEncoder, że kolumny nazywa kolejnymi cyframi. Funkcja get_feature_names_out pozwala odczytać ich nazwy. Aha i jeszcze jedna kwestia, wynikowa tablica jest typu NumPy array, stąd też jeżeli dalej do opracowania modelu potrzebny jest obiekt ramki danych nie mozna zapomnieć o przekonwerotwaniu tablicy.

Kodowanie One-Hot Encoding dla najpopularniejszych kategorii

W sytuacji gdy w zmiennej kategorialnej mamy sporą ilość kategorii, ale część z nich pojawia się rzadko warto rozważyć zmniejszenie ilości kategorii poprzez wybór jedynie tych, które występują najczęściej. Wówczas podczas kodowania za pomocą metody One Hot Encoding znacząco zmniejszymi ilość kolumn w naszym zbiorze danych. Wyobraźmy sobie, że chcemy dokonać kodowania dla dziesięciu najczęściej wystepujących kategorii w zmiennych. Zatem tym razem wybierzmy dla przykładu zmienne ’Neighborhood’, 'Exterior1st’ oraz 'Exterior2nd’. Identyfikacja ilości kategorii w nich wskazuje, ze dla zmiennej ’Neighborhood’ mamy 25 kategorii, dla drugiej zmiennej 15 i dla trzeciej 16. A my chcemy przekodować tylko dziesięć i to tych najczęściej w naszej zmiennej występującej. Zdefiniujemy zatem dwie funkcje. Jedna find_top_categories bedzie nam zwracała dziesięć najczęściej występujących kategorii w zmiennej, a druga onehot_encode tworzyć bedzie binarny wektor reprezentujący tę kategorię. Nasz kod wygląda zatem tak:

W rezultacie zamiast 51 nowych kolumn otrzymujemy 30 kolumn.

Kodowanie kategorii wartością liczbową (liczba wystąpień, częstotliwość, średnia, itp.)

To rozwiązanie ma swoje zastosowanie przy algorytmach opartych na drzewach decyzyjnych. Natomiast nie nadaje się w przypadku stosowania modeli liniowych. Generalnie intencją jest zastąpienie kategorii poprzez wartość liczbową reprezentującą określoną wielkość w zmiennej kategorialnej. Jest tu jednak pewnien szkopuł, jeżeli okaże się, że dwie lub więcej kategorii wystąpuje tyle samo razy, dają w wyniku tą samą średnią to takie kodowanie może wpłynąć na utratę cennej informacji, gdyż te kategorie zostaną zakodowane w identyczny sposób. Także trzeba o tym pamiętać.

W ten sam sposób zamiast ilości wystapień możemy użyć częstość występowania. Spotkać można także kodowanie za pomocą średniej pochodzacej ze zmiennej zależnej.

Jako uzupełniający materiał polecam kilka artykułów:

UWAGA: I na koniec powtórzę uwagę, którą mocno zaakcentowałem w poprzednim wpisie. Podobnie jak operacja uzupełniania brakujących danych, tak i kodowanie zmiennych powinno zostać zrealizowane na zbiorze danych uczących, i dopiero potem przetransponowane na zbiór testowy.