Czy zużycie energii elektrycznej zależy od temperatury zewnętrznej? Odpowiedź na to pytanie wydaje się być oczywistą. Im niższa temperatura na zewnątrz tym energii potrzebować będziemy więcej, bo przecież z jednej strony zapewnić musimy zasilanie urządzeń grzewczych, z drugiej niska temperatura to okres zimowy, co wiąże się także ze zwiększonym zapotrzebowaniem na oświetlenie. Latem z kolei mamy zapotrzebowanie na chłód, gdyż coraz częściej zaczynają nam doskwierać wysokie temperatury. Zatem … oczywista oczywistość. A może jednak nie.
Aby to sprawdzić zaprzęgniemy do pracy środowisko R. W tym miejscu skorzystam z danych o miesięcznym zużyciu energii elektrycznej [GWh], które wykorzystałem we wpisie dotyczącym prognozy zużycia energii i zestawię je ze średnią miesięczną temperaturą obliczoną ze stacji meteorologicznych umiejscowionych na obszarze kraju. Dane te publikuje Instytut Meteorologii i Gospodarki Wodnej Państwowego Instytutu Badawczego. Dane są dostępne w postaci plików zip dla poszczególnych lat. Zatem najpierw trzeba je pobrać, rozpakować a następnie wyciągnąć z nich dane o średnich miesięcznych temperaturach, i obliczyć wartość średnią dla obszaru Polski. Zatem do dzieła.
# pobieramy dane z lat 2005 do 2019
for (rok in 2005:2019) {
url <- paste0("https://dane.imgw.pl/data/dane_pomiarowo_obserwacyjne/dane_meteorologiczne/miesieczne/klimat/",rok,"/",rok,"_m_k.zip")
download.file(url, paste0(rok,"_m_k.zip"), mode = "wb")
unzip(paste0(rok,"_m_k.zip"))
}
# tworzymy ramke danych zawierajaca wszystkie dane z wybranego okresu
temperatura <- data.frame()
for (rok in 2005:2019) {
plik <- paste0("k_m_t_",rok,".csv")
df <- read.csv2(plik,header=FALSE,sep = ',',dec = '.')
temperatura <- rbind(temperatura,df)
}
temperatura_df <- temperatura[,c(3:5)]
colnames(temperatura_df) <- c("Rok","Miesiac","Temperatura")
temperatura_df %>%
group_by(Rok, Miesiac) %>%
summarise(
Temp = mean(Temperatura, na.rm = TRUE)
) -> temperatura.srednia
temperatura = as_vector(temperatura.srednia $Temp)
Następnie tworzę ramkę danych, która zawierać będzie wyznaczone dane o średniej miesięcznej temperaturze z lat 2005-2019 i odpowiadającym jej miesięcznym zużyciu energii elektrycznej w GWh.
dane <- as.data.frame(cbind(zuzycie, temperatura))
colnames(dane) <- c('zuzycie','temperatura')
Mając przygotowane dane możemy przystąpić do oceny związku pomiędzy tymi dwoma zmiennymi. W matematyce mówimy o współzależności, korelacji między zmiennymi. Zależność tą opisuje współczynnik korelacji. Istnieje wiele różnych wzorów dla współczynników korelacji. Najbardziej znanymi są:
- współczynnik korelacji Pearsona
- współczynnik korelacji rang Spearmana
- współczynnik korelacji tau Kendalla
Wymienione współczynniki poddane zostały normalizacji, także przybierają wartości od −1 (zupełna korelacja ujemna), przez 0 (brak korelacji) do +1 (zupełna korelacja dodatnia).
W środowisku R współczynniki korelacji można wyznaczyć za pomocą funkcji cor() lub cor.test(). Różnica między nimi jest taka, że pierwsza podaje w wyniku obliczone współczynniki, druga oblicza współczynniki przy jednoczesnym przeprowadzeniu testu oceny współzależności pomiędzy badanymi zmiennymi.
Ale za nim przystąpimy do wyznaczenia współczynników korelacji zerknijmy na dane, gdyż czasami wystarczy przysłowiowy rzut oka aby dostrzec określone zależności. Tak przy okazji wykorzystam po raz pierwszy graficzną bibliotekę ggpubr opracowaną przez Alboukadela Kassambara.
Biblioteka stanowi zbiór funkcji upraszczających tworzenie wykresów w oparciu o bibliotekę ggplot2, która w swojej konstrukcji wymaga pewnych umiejętności i wiedzy na temat tworzenia wykresów. Ostatnią wersję biblioteki ggpubr można pobrać z GitHub autora wydając następujące polecenie:
if(!require(devtools)) install.packages("devtools") devtools::install_github("kassambara/ggpubr")
Zatem jak wygląda wykres punktowy utworzony przez funkcję ggscatter(). Dlaczego wykres punktowy? A dlatego, że łatwo sprawdzić czy występuje właśnie zależność między zmiennymi, jaki ma ona kierunek, a nawet jaka jest siła relacji między badanymi zmiennymi. Pokazuje także czy przypadkiem nie występują przypadki nietypowe (ang. outliers), które mogłyby zakłócić wartość współczynnika korelacji.
ggscatter(dane, x = "temperatura", y = "zuzycie",
color ="black",
size = 2,
title = "Zużycie energii elektrycznej w funkcji średniej miesięcznej temperatury zewnętrznej",
xlab = "Średnia miesięczna temperatura, C", ylab = "Zużycie energii elektrycznej, GWh")
Spójrzmy zatem na uzyskany wykres zależności pomiędzy średnią miesięczną temperaturą a miesięcznym zużyciem energii elektrycznej.
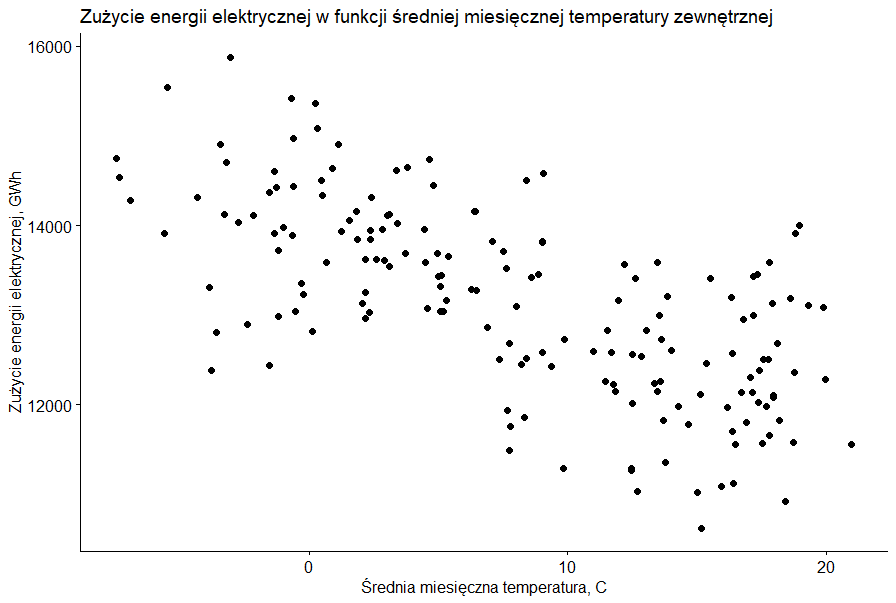
I już widzimy, że można się doszukać ujemnej korelacji pomiędzy tymi dwoma zmiennymi. Im wyższa temperatura tym mniejsze zużycie energii elektrycznej. Ale spokojnie, bo jeszcze doszlibyśmy do wniosku, że jak już będzie wysoka temperatura to i energii nie będziemy wcale potrzebować. Może to i prawda, bo przy tak wysokiej temperaturze może nas już wcale nie będzie. Zresztą jeżeli przyjrzeć się bliżej rozkładowi zużycia energii elektrycznej dla określonych zakresów średniej temperatury miesięcznej to widać, że dla temperatur powyżej 16,9°C mediana zużycia energii lekko zaczyna rosnąć. I tego kierunku ze zwięszeniem energii elektrycznej na potrzeby chłodu byśmy oczekiwali.
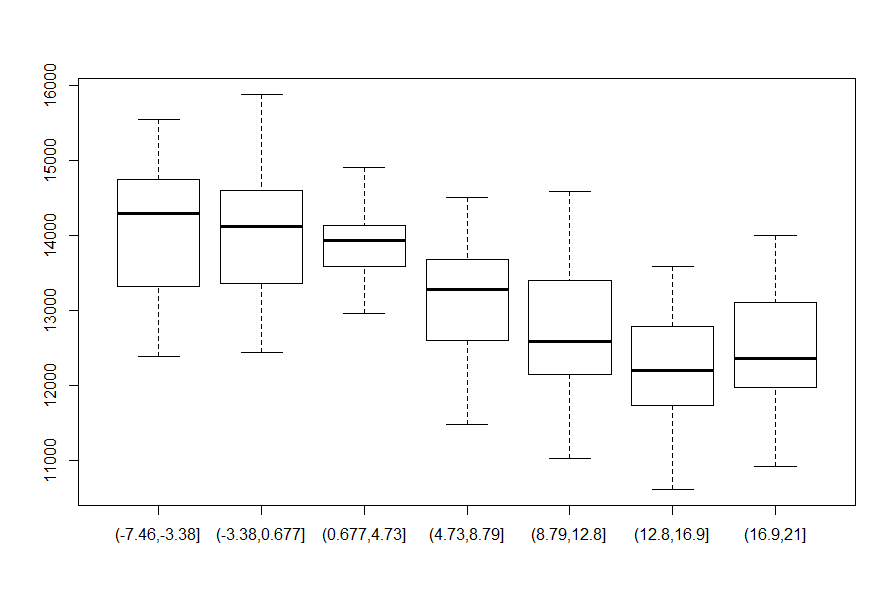
Wróćmy jednak do naszego wykresu punktowego i spróbujmy na niego nanieść trend liniowy, przy okazji wstępnie obliczymy także współczynnik korelacji ran Spearmana. Dlaczego akurat ten a nie inny o tym trochę później, teraz wpisujemy kod.
ggscatter(dane, x = "temperatura", y = "zuzycie",
color ="black",
size = 2,
add = "reg.line",
conf.int = TRUE,
add.params = list(color = "blue",fill = "lightgray"),
cor.coef = TRUE,
cor.coeff.args = list(method = "spearman", label.x = 0, label.y= 11500, label.sep = "\n"),
title = "Zużycie energii elektrycznej w funkcji średniej miesięcznej temperatury zewnętrznej",
xlab = "Średnia miesięczna temperatura, C", ylab = "Zużycie energii elektrycznej, GWh")
I mamy wykres punktowy z linią trendu o ujemnym współczynniku nachylenia.
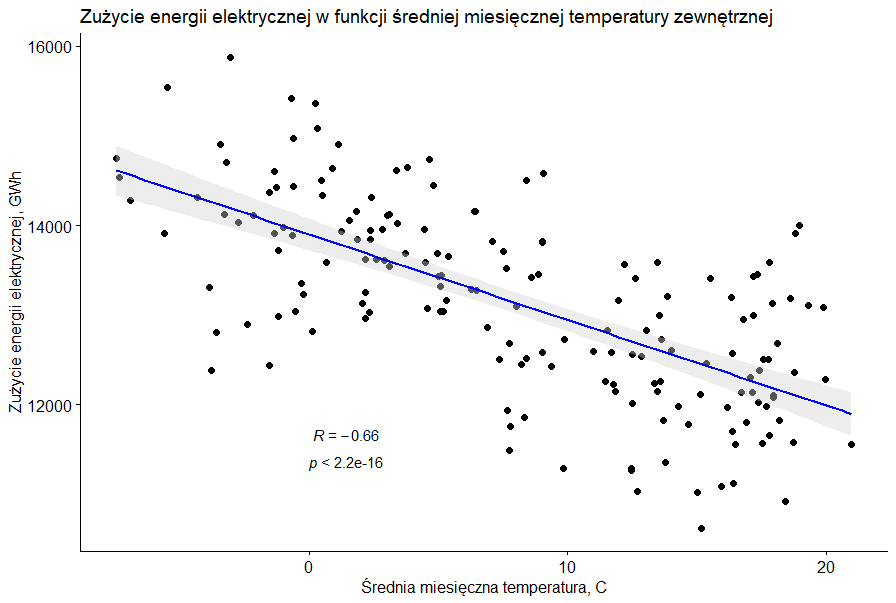
Potwierdziły się zatem nasze pierwotne spostrzeżenia. A ponieważ obliczona wartość współczynnika korelacji wynosi 0,66 mamy do czynienia z umiarkowaną zależnością. Obliczmy zatem wszystkie współczynniki korelacji wymienione na początku wpisu.
# obliczanie współczynnika korelacji dla poszczególnych metod
cor(zuzycie, temperatura, method = c("pearson"))
cor(zuzycie, temperatura, method = c("spearman"))
cor(zuzycie, temperatura, method = c("kendall"))
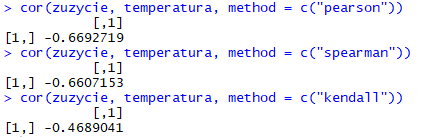
Wartości współczynników są ujemne, co oznacza, że jeżeli jedna zmienna rośnie to druga maleje. Żeby wyznaczyć współczynnik korelacji musimy jednak pamiętać o kilku podstawowych założeniach. Przede wszystkim musimy mieć do czynienia z cechami mierzalnymi, i to w naszym przypadku jest spełnione. Ważny jest rodzaj cech (interwałowa, proporcjonalna), a dla współczynnika korelacji Pearsona cecha musi mieć rozkład normalny lub zbliżony do normalnego. Pamiętajmy również o tym, że współczynnik korelacji Pearsona liczy korelację liniową. Stąd przeprowadzimy obecnie testy, by sprawdzić normalność rozkładu naszych zmiennych. Aby sprawdzić czy rozkład jest normalny możemy wstępnie posłużyć się parametrami statystyki opisowej takimi jak skośność czy kurtoza, ale najczęściej sprawdzimy to korzystać z wykresu normalności czy też stosując odpowiedni test, np. test Shapiro-Wilka. Do wykreślenia wykresu normalności skorzystam z funkcji ggqqplot() z pakietu ggpubr, a test Shapiro-Wilka przeprowadzę korzystając z funkcji shapiro.test().
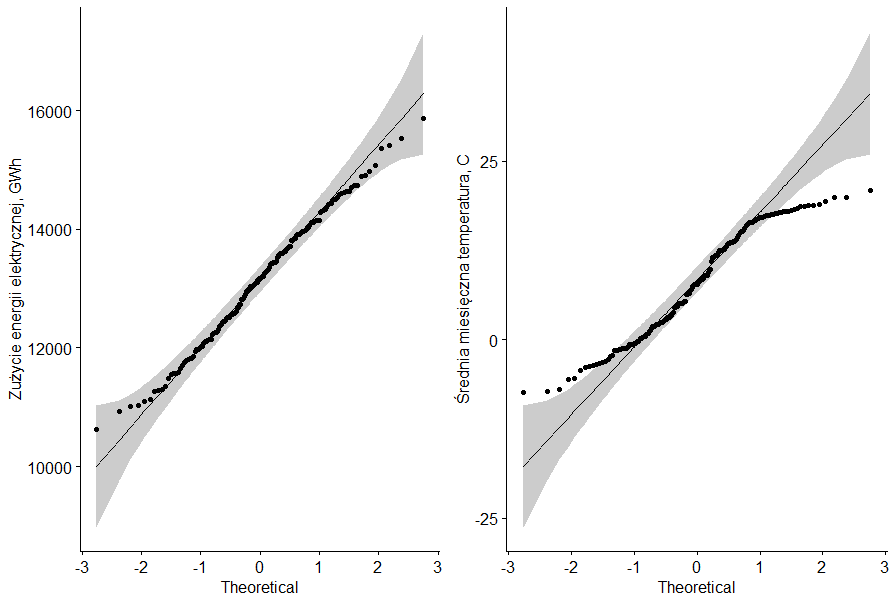
Wizualna ocena normalności rozkładu zmiennych pozwala na stwierdzenie, że o ile w przypadku zmiennej zużycia energii elektrycznej nie ma wątpliwości co do charakteru jego rozkładu to w przypadku zmiennej średniej miesięcznej temperatury niewątpliwie taka wątpliwość już istnieje. Przeprowadzamy zatem test Shapiro-Wilka zarówno tak dla jednej jak i dla drugiej zmiennej.
# test Shapiro-Wilka dla zmiennej zuzycie
shapiro.test(dane$zuzycie) # => p = 0.66
# test Shapiro-Wilka dla zmiennej temperatura
shapiro.test(dane$temperatura) # => p = 1.677e-05
Z uzyskanych wartości prawodopodobieństwa komputerowego stwierdzamy, że o ile dla zmiennej zużycie nie ma podstaw do odrzucenia hipotezy o normalności rozkładu, to już w przypadku zmiennej temperatura hipoteza o normalności rozkładu musi być odrzucona. Stąd niespełnienie założenia o normalności rozkładu nie pozwala nam zastosować metody Pearsona, gdyż ta jak zaznaczyłem wcześniej może być stosowana gdy obie badane zmienne mają rozkład normalny. Taki warunek nie występuje dla metody Spearmana czy Kendalla gdyż są to testy nieparametryczne. Przeprowadźmy je zatem.
cor.test(dane$zuzycie, dane$temperatura, method = "spearman")

Współczynnik korelacji rang Spearmana pomiędzy zmienną „zużycie energii elektrycznej”, a zmienną „średnia temperatura misięczna” wynosi -0,66, a wartość prawdopodobieństwa komputerowego jest mniejsza niż 0,05 i wynosi 2.2e-16. Stąd wnioskujemy, że zmienne są ze sobą skorelowane umiarkowanie.
cor.test(dane$zuzycie, dane$temperatura, method = "kendall")

Wartość współczynnika korelacji wg Kendalla wynosi -0,4689, a wartość prawdopodobieństwa komputerowego jest mniejsza niż 0,05 i wynosi 2.2e-16. Wniosek podobnie jak wyżej – zmienne są ze sobą skorelowane umiarkowanie.






