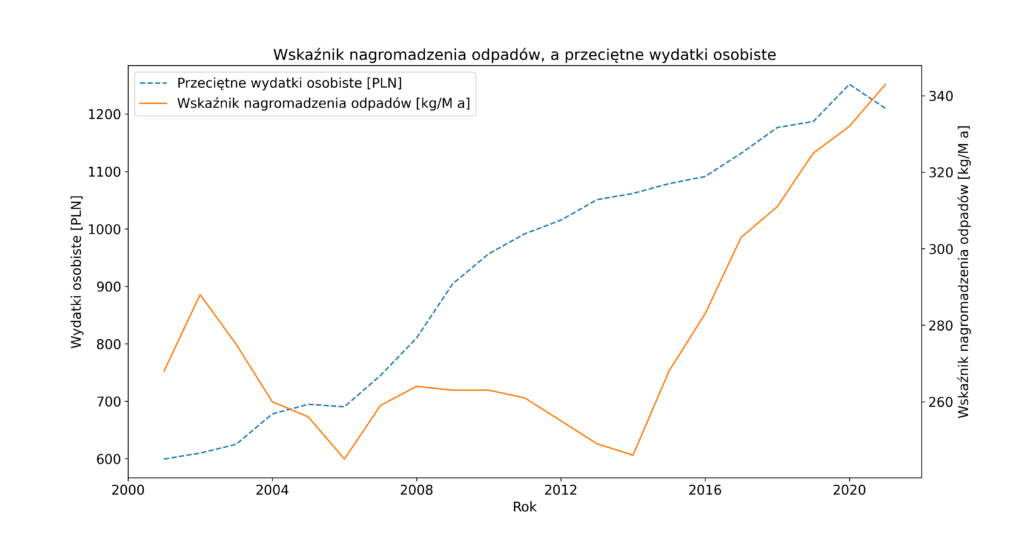
Rok 2020 to kolejny rok, w którym wskaźnik masowy nagromadzenia odpadów odniesiony do jednego mieszkańca, czyli ogólnie mówiąc wskaźnik pokazujący ile odpadów wytwarza każdy z nas, osiągnął kolejny rekord. Na jednego mieszkańca przypadało w 2020 r. średnio 342 kg wytworzonych odpadów komunalnych, co oznacza wzrost o około 10 kg w porównaniu z rokiem poprzednim. A jeszcze w 2010 roku wartość tego wskaźnika wynosiła około 263 kg. W ciągu dziesięciu lat statystyczny mieszkaniec Polski zwiększył ilość wytwarzanych odpadów komunalnych o blisko 80 kg. I co najgorsze w tym wszystkim, to że ciągle wytwarzamy jako Polacy mniej niż statystyczny Europejczyk. Dla przypomnienia średnia unijna wynosi 502 kg [2]
Z kolei jak wynika z raportu „Sytuacja gospodarstw domowych w 2020 r. w świetle badania budżetów gospodarstw domowych”[1] opublikowanego przez Główny Urząd Statystyczny sytuacja materialna gospodarstw domowych nieznacznie poprawiła się pomimo pandemii COVID-19. Gospodarstwa domowe osiągnęły wyższe dochody. Nadal jednak utrzymuje się relatywnie duże zróżnicowanie przeciętnych miesięcznych dochodów pomiędzy różnymi grupami społeczno-ekonomicznymi. Oczywiście wzrost dochodów przekłada się na wzrost wydatków, choć należy zauważyć, że przeciętne miesięczne wydatki na 1 osobę w gospodarstwach domowych w 2020 roku były realnie niższe o 6,5% (nominalnie o 3,4%) od wydatków z 2019 roku. Wydajemy więcej przede wszystkim na dobra konsumpcyjne, żywność, napoje bezalkoholowe itp. Także nie dziwi fakt, że i odpadów komunalnych nam przybywa.
Model wektorowej autoregresji (VAR)
Postanowiłem zatem sprawdzić, jak sprawdzi się model wektorowej autoregresji w prognozowaniu przyszłych wartości tych wskaźników. Dla nie wtajemniczonych model wektorowej autoregresji, określany często w literaturze jako VAR [3] (ang. vector autoregression), jest stochastycznym modelem ekonometrycznym szeroko stosowanym w ekonomii czy naukach przyrodniczych. Przykłady zastosowania modeli VAR można znaleźć zarówno w literaturze polskiej, jak i w światowej. Model VAR uogólnia model autoregresji z jedną zmienną (jednowymiarową) na wielowymiarowe szeregi czasowe. K-wymiarowy model VAR rzędu p oznaczony jako VAR(p) dla dwóch zmiennych i jednym opóźnieniu (czyli VAR(1)) można przedstawić jako następujący układ równań:
𝑦1,𝑡=𝑐1+𝜙11,1𝑦1,𝑡−1+𝜙12,1𝑦2,𝑡−1+𝜀1,𝑡
𝑦2,𝑡=𝑐2+𝜙21,1𝑦1,𝑡−1+𝜙22,1𝑦2,𝑡−1+𝜀2,𝑡
gdzie:
– 𝑦k,𝑡 jest k wymiarowym szeregiem czasowym jednowymiarowej zmiennej,
– 𝜙𝑖𝑖,𝑙 określają wpływ 𝑙-tego opóźnienia zmiennej 𝑦i na nią samą,
– 𝜙𝑖𝑗,𝑙 określają wpływ 𝑙-tego opóźnienia zmiennej 𝑦𝑗 na zmienną 𝑦𝑖,
– współczynniki 𝜀1,𝑡 i 𝜀2,𝑡 stanowią błąd (szum biały), który może być skorelowany.
Dane do analizy
Dane do analizy zostały pobrane z Banku Danych Lokalnych [4] i stanowią roczne wartości przeciętnych miesięcznych wydatków na 1 osobę w gospodarstwie domowym oraz wskaźnika nagromadzenia odpadów przypadający na 1 osobę w gospodarstwie domowym w ostatnim dwudziestoleciu, czyli w latach 2000-2020. Na rysunku 1 przedstawiono jak kształtowały się te dwa wskaźniki na przestrzeni oznaczonych lat.
Środowisko analizy
Do przeprowadzenia analizy wykorzystano środowisko Jupyter Notebook, a w nim bibliotekę statsmodels [5], która dostarcza szeregu klas i funkcji do szacowania wielu różnych modeli statystycznych, w tym także modelu wektorowej autoregresji [6]
Zaczynamy
Wczytujemy zatem potrzebne biblioteki oraz pozyskane dane do analizy przy okazji nadając im odpowiedni typ szeregu czasowego datetime64 [7] oraz określając ich częstotliwość jako roczną.
# Load basic libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# Load specific forecasting tools. From statsmodels.tsa.api import VAR model
from statsmodels.tsa.vector_ar.var_model import VAR, VARResults
from statsmodels.tsa.stattools import adfuller
from statsmodels.tools.eval_measures import rmse
# Ignore harmless warnings
import warnings
warnings.filterwarnings("ignore")
# Load datasets
df = pd.read_csv("wskaznik_nagromadzenia_a_wydatki_na_osobe.csv", sep=';', decimal = ',', index_col=[0], parse_dates=True)
df.index.freq = 'A-DEC'
df.index.names = ['Year']
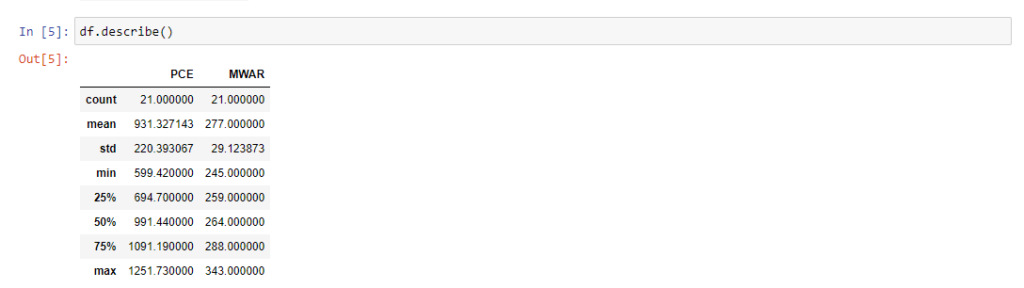
Krótki rzut oka na statystyczne parametry opisowe naszych zmiennych. Jako PCE oznaczono przeciętne, miesięczne wydatki osobiste, a jako MWAR wskaźnik nagromadzenia odpadów. Mamy zatem po 21 danych w obu seriach, średnia wartość dla wydatków osobistych na przestrzeni 20 ostatnich lat wynosi 931 zł, a średni wskaźnik nagromadzenia odpadów 277 kg na mieszkańca na rok.
Czy szeregi są stacjonarne?
Przystępując do przeprowadzenia analizy z wykorzystaniem modelu autoregresyjnego musimy pamiętać o kilku rzeczach. Na początku należy sprawdzić, czy szeregi czasowe naszych zmiennych endogenicznych są stacjonarne. W tym celu skorzystałem z rozszerzonego testu Dickeya-Fullera (tzw. test ADF – ang. Augmented Dickey-Fuller test), który służy statystycznej weryfikacji stacjonarności i jest zaimplementowany w bibliotece stattools [8]. Generalnie jeżeli obliczona wartość statystyki testu ADF jest większa niż wartość krytyczna to nie ma podstaw do odrzucenia hipotezy zerowej o niestacjonarności badanej zmiennej. Jeśli obliczona wartość statystyki testu ADF jest mniejsza niż wartość krytyczna, hipotezę zerową odrzucamy na rzecz stacjonarności zmiennej.
def adf_test(series,title=''):
"""
Pass in a time series and an optional title, returns an ADF report
"""
print(f'Augmented Dickey-Fuller Test: {title}')
result = adfuller(series.dropna(),autolag='AIC') # .dropna() handles differenced data
labels = ['ADF test statistic','p-value','# lags used','# observations']
out = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
out[f'critical value ({key})']=val
print(out.to_string()) # .to_string() removes the line "dtype: float64"
if result[1] <= 0.05:
print("Strong evidence against the null hypothesis")
print("Reject the null hypothesis")
print("Data has no unit root and is stationary")
else:
print("Weak evidence against the null hypothesis")
print("Fail to reject the null hypothesis")
print("Data has a unit root and is non-stationary")
adf_test(df['MWAR'],title='Waste')
adf_test(df['PCE'],title='Spending')
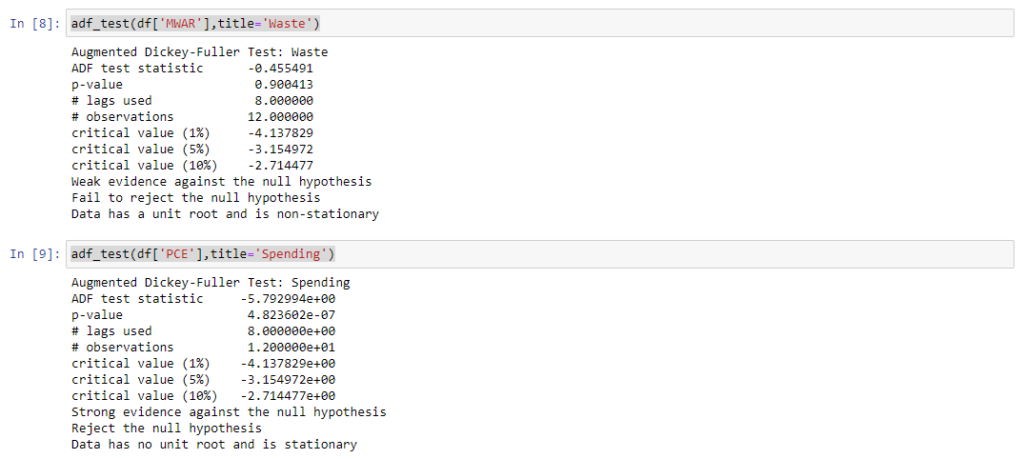
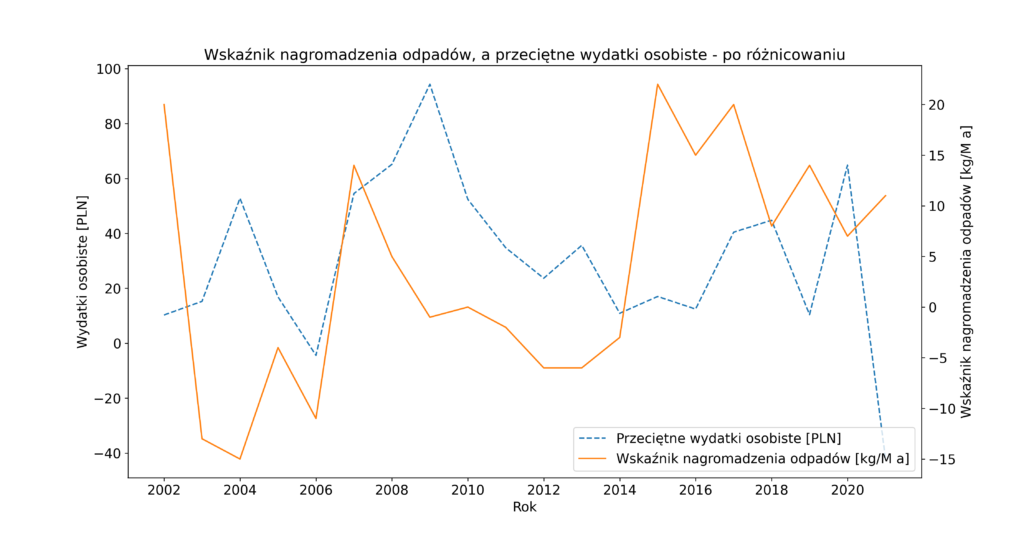
Jak się okazało zmienna endogeniczna – wskaźnik nagromadzenia odpadów – okazała się szeregiem niestacjonarnym, co wymusiło przeprowadzenie różnicowania szeregów czasowych i ponowne wykonanie testu ADF. To jednak również nie wystarczyło, konieczne było przeprowadzenie powtórnego różnicowania. Dopiero na tym etapie ustabilizowano szeregi czasowe, niestety zostało to okupione utratą wartości z dwóch początkowych lat. W rezultacie do dalszego szacowania modelu wykorzystano drugie różnice zmiennych.
Podział na zbiór uczący i testowy
Kolejnym krokiem był podział posiadanego zbioru na zbiór uczący oraz testowy. Jako zbiór uczący wybrano początkowe 17 wartości, a zbiór testowy stanowiły wartości z roku 2019 oraz 2020.
nobs=2
train, test = df_transformed[:-nobs], df_transformed[-nobs:]
Rząd i parametry modelu VAR
Wybór początkowego rzędu dla modelu VAR oparty został o kryterium informacyjne Akaikego (AIC) [9] oraz bayesowskie kryterium informacyjne Schwartza (BIC) [10].
for i in range(5):
model = VAR(train)
results = model.fit(i)
print('Order =', i)
print('AIC: ', results.aic)
print('BIC: ', results.bic)
print('HQIC: ', results.hqic, '\n')
print()
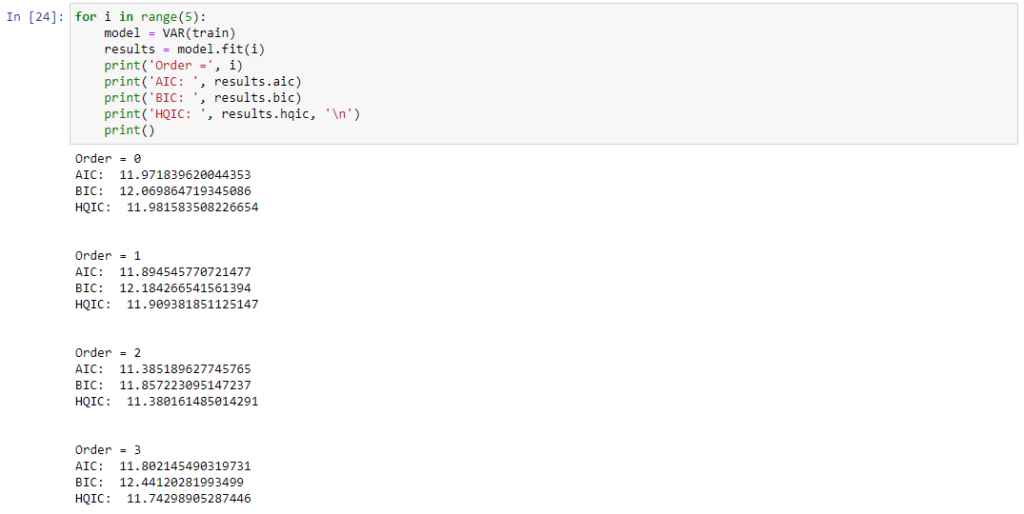
Najmniejsze wartości dla wyznaczonych kryterium wskazały na drugi rząd opóźnienia. Parametry modelu VAR(2) przedstawiono poniżej.
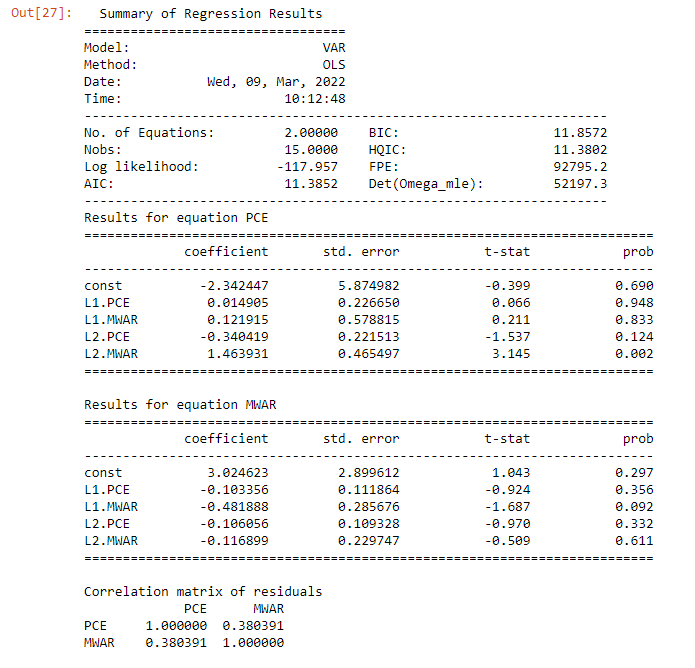
Zdecydowanie zauważamy, ze większościowo zmiany predyktora nie są związane ze zmianami w odpowiedzi. Celem stwierdzenia, czy szereg czasowy wskaźnika nagromadzenia odpadów jest użyteczny w prognozowaniu szeregu czasowego wydatków osobistych przeprowadziłem liniowy test przyczynowości Grangera. Postawiona hipoteza zerowa oznacza brak zależności przyczynowej w sensie Grangera jednej zmiennej od drugiej, w przeciwieństwie do hipotezy alternatywnej która oznacza przyczynową zależność, czyli to, ze wartość zmiennej w jednym szeregu przy określonym opóźnieniu może być znacząca dla prognozowania wartości zmiennej w drugim szeregu w późniejszym okresie [11]. Oczywiście hipotezę zerową odrzucamy dla p-value < 0.05. Wynik testu wskazał, ze wydatki osobiste nie wykazują zależności przyczynowej z wskaźnikiem nagromadzenia odpadów,

ale pomiędzy wskaźnikiem nagromadzenia odpadów a wydatkami osobistymi takiej przyczynowości możemy się doszukać.

Przeprowadzono także test Portmanteau do zbadania czy występuje autokorelacja reszt po dopasowaniu modelu. Dla m>2 wartość p < 0.05, tak więc nie mamy do czynienia z autokorelacją reszt.

Testujemy model
Zatem można teraz przejść do przetestowania zbudowanego modelu wykorzystując do tego zbiór testowy i funkcję forecast. Do funkcji przekazać należy wprost rząd opóźnienia. A z powodu tego, ze narzędzie nie określa wprost indeksu czasowego musimy to zrobić ręcznie.
lag_order = results.k_ar
z = results.forecast(y=train.values[-lag_order:], steps=2)
idx = pd.date_range('31/12/2019', periods=2, freq='A-DEC')
df_forecast = pd.DataFrame(z, index=idx, columns=['Spending2d','Waste2d'])
Oczywiście otrzymane wartości stanowią drugie różnice zmiennych, zatem celem porównania należało wykonać odwrotne podwójne różnicowanie.
# Add the most recent first difference from the training side of the original dataset to the forecast cumulative sum
df_forecast['Spending1d'] = (df['PCE'].iloc[-nobs-1]-df['PCE'].iloc[-nobs-2]) + df_forecast['Spending2d'].cumsum()
# Now build the forecast values from the first difference set
df_forecast['PCE_Forecast'] = df['PCE'].iloc[-nobs-1] + df_forecast['Spending1d'].cumsum()
# Add the most recent first difference from the training side of the original dataset to the forecast cumulative sum
df_forecast['Waste1d'] = (df['MWAR'].iloc[-nobs-1]-df['MWAR'].iloc[-nobs-2]) + df_forecast['Waste2d'].cumsum()
# Now build the forecast values from the first difference set
df_forecast['MWAR_Forecast'] = df['MWAR'].iloc[-nobs-1] + df_forecast['Waste1d'].cumsum()
Oszacowanie mierników
W rezultacie otrzymano wartości z modelu, które porównano z wartościami zbioru testowego współczynnika nagromadzenia odpadów i przeciętnych, osobistych, miesięcznych wydatków. Błąd oszacowano za pomocą RMSE (ang. root mean square error) [1] oraz innych statystycznych mierników, takich jak: MAPE, MAE, MPE.
from statsmodels.tsa.stattools import acf
def forecast_accuracy(forecast, actual):
mape = np.mean(np.abs(forecast - actual)/np.abs(actual)) # MAPE
me = np.mean(forecast - actual) # ME
mae = np.mean(np.abs(forecast - actual)) # MAE
mpe = np.mean((forecast - actual)/actual) # MPE
rmse = np.mean((forecast - actual)**2)**.5 # RMSE
corr = np.corrcoef(forecast, actual)[0,1] # corr
mins = np.amin(np.hstack([forecast[:,None],
actual[:,None]]), axis=1)
maxs = np.amax(np.hstack([forecast[:,None],
actual[:,None]]), axis=1)
minmax = 1 - np.mean(mins/maxs) # minmax
return({'mape':mape, 'me':me, 'mae': mae,
'mpe': mpe, 'rmse':rmse, 'corr':corr, 'minmax':minmax})
print('Forecast Accuracy of: PCE')
accuracy_prod = forecast_accuracy(df_forecast['PCE_Forecast'].values, df['PCE'][-nobs:])
for k, v in accuracy_prod.items():
print(k, ': ', round(v,4))
print('\nForecast Accuracy of: MWAR')
accuracy_prod = forecast_accuracy(df_forecast['MWAR_Forecast'].values, df['MWAR'][-nobs:])
for k, v in accuracy_prod.items():
print(k, ': ', round(v,4))
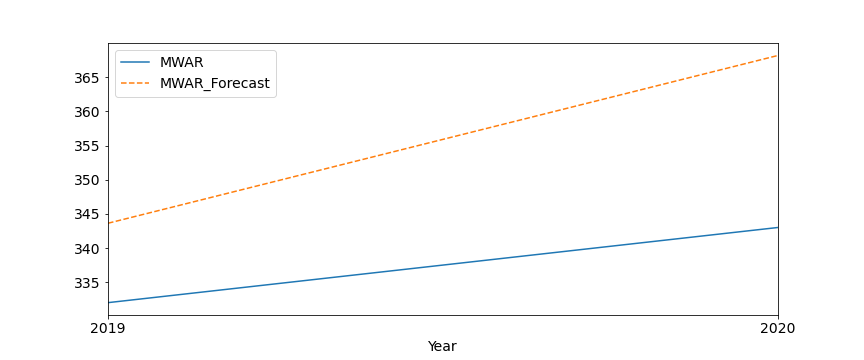
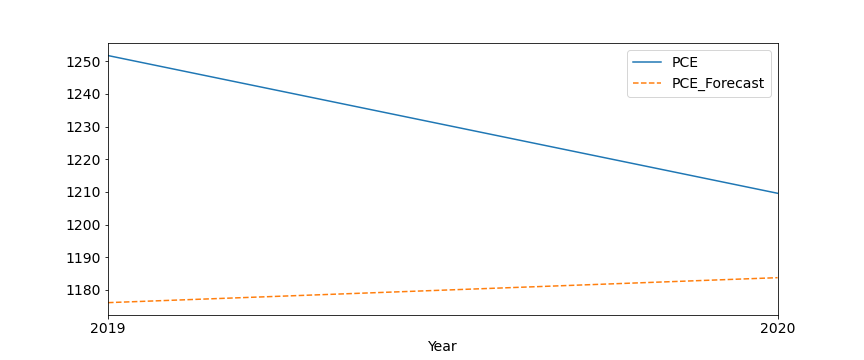
Wartość błędu średniokwadratowego dla współczynnika nagromadzenia odpadów wyniosła 19.614 kg przy średniej wartości 337.5 kg, z kolei dla przeciętnego miesięcznego wydatku osobistego 56.51 zł przy średniej wartości 1230.66 zł. Stąd tez względny błąd prognozowania nie przekracza 7%, przez co model prognozowania jest do przyjęcia.
Prognoza na trzy lata
Wyznaczmy zatem w oparciu o niego przyszłe wartości, np na lata 2021-2023. Jak z nich widać uzyskano dość znaczący wzrost w przypadku współczynnika nagromadzenia odpadów. Szacowana wartość parametru na koniec 31 grudnia 2021 wyniosła 346,2 kg. Z kolei w przypadku przeciętnych miesięcznych wydatków obserwujemy początkowy spadek wskaźnika w stosunku do lat ostatnich. Potem lekki wzrost. A jak będzie, to już za kilka miesięcy będziemy mogli to zweryfikować.
[1] https://stat.gov.pl/obszary-tematyczne/warunki-zycia/dochody-wydatki-i-warunki-zycia-ludnosci/sytuacja-gospodarstw-domowych-w-2020-r-w-swietle-badania-budzetow-gospodarstw-domowych,3,20.html
[2] https://ekordo.pl/statystyka-odpadowa-wg-danych-eurostatu-za-2019-r/
[3] https://en.wikipedia.org/wiki/Vector_autoregression
[4] https://bdl.stat.gov.pl/BDL/start
[5] Introduction — statsmodels
[6] Vector Autoregressions tsa.vector_ar — statsmodels
[7] Time series / date functionality — pandas 1.4.1 documentation (pydata.org)
[8] statsmodels.tsa.stattools — statsmodels
[9] https://pl.wikipedia.org/wiki/Kryterium_informacyjne_Akaikego
[10] https://pl.wikipedia.org/wiki/Bayesowskie_kryterium_informacyjne_Schwarza




